Narysuj dwie proste m i k, które przecinają się w punkcie S, aby jeden kąt między prostymi był równy 60°. Na narysowanych prostych zaznacz w tej samej odległości od punktu S punkty: M, N, O i P Połącz kolejne punkty i oblicz miary kątów wewnętrznych wszystkich utworzonych trójkątów i nazwij je. Napisz, która z utworzonych figur jest osiowosymetryczna.
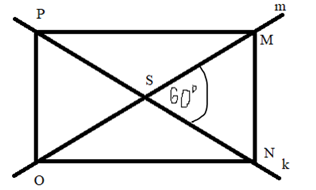
Kąt SMN jest równy kątowi SNM i jest równy:
(180° – 60°): 2 = 120°: 2 = 60°
Kąt PSM jest równy:
180° – 60° = 120°
Kąt SPO i SMP są równe:
(180° – 120°): 2 = 60°: 2 = 30°
Trójkąty równoboczne ostrokątne: SMN, PSO.
Trójkąty różnoboczny prostokątny: MNO, PNO, NMP, MPO.
Trójkąty równoramienne rozwartokątne: OSN, MSP

Kąty PSM i MSN to kąty przyległe, których suma jest równa 180°. Skorzystaj z tego, że suma miar kątów w trójkącie wynosi
![]() , a miary kątów przy podstawie trójkątów równoramiennych są równe.
, a miary kątów przy podstawie trójkątów równoramiennych są równe.

Zadanie 1
60Zadanie 11
61Zadanie 14
62Zadanie 6
71Zadanie 19
73Zadanie 20
73Zadanie Problem
74Zadanie 7
78Zadanie 11
79Zadanie 16
79Zadanie 7
83Zadanie 15
84Zadanie 19
85Zadanie A to ciekawe! 3
85Zadanie Problem
86Zadanie 1
87Zadanie 5
87Zadanie 7
87Zadanie 11
88Zadanie 12
88Zadanie 13
88Zadanie 19
89Zadanie 20
89
