Odczytaj z wykresu, momenty, w których zmieniała się wypadkowa oraz oblicz wartość siły w kolejnych okresach czasu i sporządź jej wykres.
Wypadkowa zmieniała się w chwili
![]() = 2 s oraz
= 2 s oraz
![]() = 6 s.
= 6 s.
DANE:
m = 2 000 kg
Δt1 = 2 s
Δt2 = 4 s
Δt3 = 2 s
Δv1 = 8
![]()
Δv2 = 4
![]()
Δv3 = 8
![]()
SZUKANE:
Fw1 = ? Fw2 = ? Fw3 = ?
WZÓR:
a =
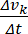
a =
![]() | ∙ m
| ∙ m
Fw = m ∙ a = m ∙
![]()
Fw1 = 2 000 kg ∙
![]() = 8 000 N = 8 kN
= 8 000 N = 8 kN
Fw2 = 2 000 kg
![]() = 2 000 N = 2 kN
= 2 000 N = 2 kN
Fw3 = 2 000 kg ∙
![]() = 8 000 N = 8 kN
= 8 000 N = 8 kN
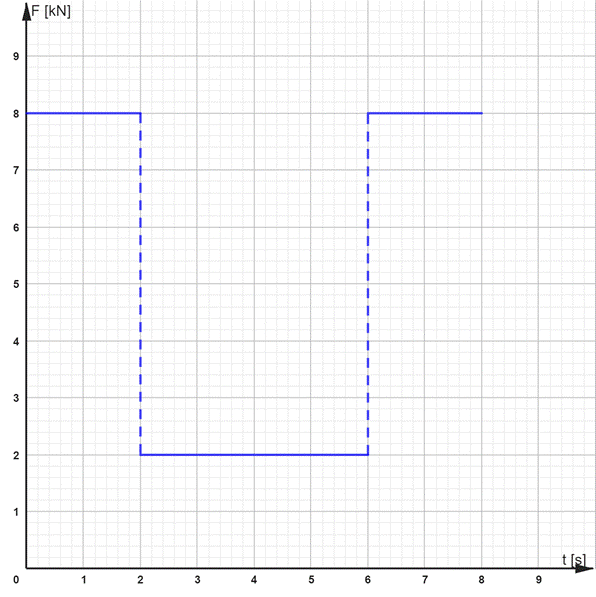

Zgodnie z drugą zasadą dynamiki, gdy na ciało działa siła wypadkowa różna od zera, to ciało porusza się z przyspieszeniem (a) wprost proporcjonalnym do siły wypadkowe (Fw) oraz odwrotnie proporcjonalnym do masy (m) ciała. W ruchu jednostajnie przyspieszonym przyspieszenie jest stosunkiem zmiany prędkości (∆v) do czasu (t), w którym ona nastąpiła. Siła wypadkowa w danym okresie czasu jest stała, więc jej wykresem jest prosta równoległa do osi czasu.

Zadanie 14.2.
56Zadanie 14.3.
56Zadanie 14.4.
57Zadanie 15.3.
58Zadanie 15.10.
59Zadanie 15.11.
59Zadanie 15.12.
60Zadanie 16.6.
61Zadanie 16.10.
62Zadanie 17.3.
63Zadanie 17.4.
63Zadanie 17.5.
63Zadanie 17.7.
63Zadanie 18.1.
65Zadanie 18.11.
66Zadanie 20.3.
70Zadanie 20.7.
70Zadanie 20.13.
71Zadanie 20.14.
71Zadanie 20.15.
72Zadanie 21.9.
73Zadanie 21.11
74Zadanie 21.12.
74Zadanie 21.13.
74Zadanie 21.14.
74Zadanie 22.6.
75Zadanie 22.7.
76Zadanie 22.10.
76Zadanie 23.1.
77Zadanie 23.2.
77Zadanie 23.6.
78Zadanie 23.10.
78Zadanie 23.11.
78Zadanie 23.12.
79
