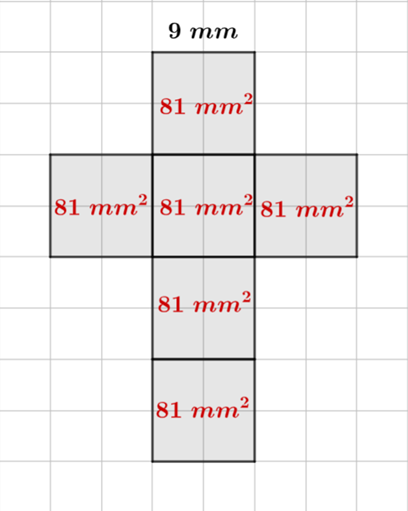
Prostopadłościan żółty:
Każda krawędź wynosi 9 mm.
Pole jednej ściany: 9 mm ⋅ 9 mm = 81 mm2
Pole całkowite: P = 6 ⋅ 81 mm2 = 486 mm2
Prostopadłościan niebieski:
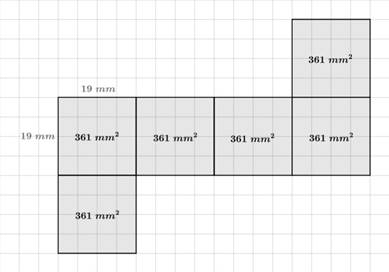
Każda krawędź wynosi 19 mm.
Pole jednej ściany: 19 mm ⋅ 19 mm = 361 mm2
Pole całkowite: P = 6 ⋅ 361 mm2 = 2166 mm2
Prostopadłościan pomarańczowy:
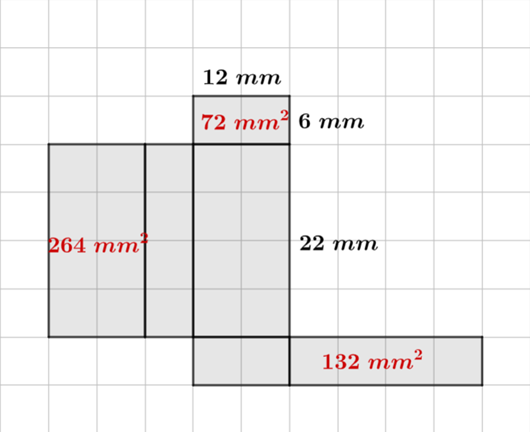
Krawędzie wynoszą: 6 mm, 12 mm, 22 mm.
Pola ścian:
6 mm ⋅ 12 mm = 72 mm2
12 mm ⋅ 22 mm = 264 mm2
22 mm ⋅ 6 mm = 132 mm2
Pole całkowite: P = 2 ⋅ 72 mm2 + 2 ⋅ 132 mm2 + 2 ⋅ 264 mm2 = 144 mm2 + 264 mm2 + 528 mm2 = 936 mm2
Prostopadłościan zielony:
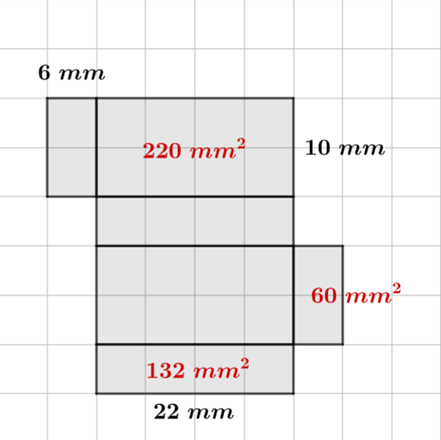
Krawędzie wynoszą: 6 mm, 12 mm, 22 mm.
Pola ścian:
6 mm ⋅ 12 mm = 72 mm2
12 mm ⋅ 22 mm = 264 mm2
22 mm ⋅ 6 mm = 132 mm2
Pole całkowite: P = 2 ⋅ 72 mm2 + 2 ⋅ 132 mm2 + 2 ⋅ 264 mm2 = 144 mm2 + 264 mm2 + 528 mm2 = 936 mm2

Na początku zmierz za pomocą linijki długości krawędzi brył – w dwóch pierwszych przypadkach są to sześciany, więc wystarczy tylko jedna krawędź. Następnie oblicz pole każdej z tych ścian, mnożąc długości krawędzi prostokątów i wyznacz pole powierzchni całkowitej, sumując pola wszystkich ścian.