W tym zadaniu musisz narysować trójkąt o powyższych wymiarach, a następnie zmierzyć wysokości nań poprowadzone.
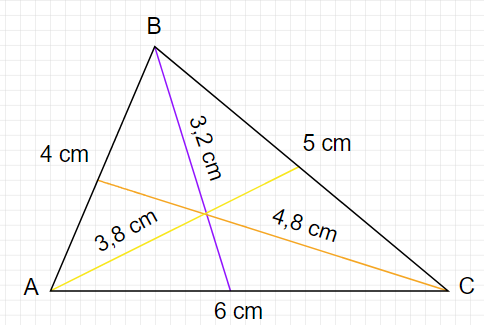
Bok AB ma 4 cm, a wysokość opuszczona na ten bok ma 4,8 cm.
Bok BC ma 5 cm, a wysokość opuszczona na ten bok ma 3,8 cm.
Bok AC ma 6 cm, a wysokość opuszczona na ten bok ma 3,2 cm.
Spośród wszystkich wysokości trójkąta ABC wysokość opuszczona na najdłuższy bok jest najkrótsza, a wysokość opuszczona na najkrótszy bok jest najdłuższa.

Powstaje tutaj pewna zależność, która będzie bardziej rozwinięta w temacie dot. pola trójkąta. Ponieważ pole trójkąta to połowa iloczynu długości boku i jego wysokości, to te iloczynu się muszą proporcjonalnie zgadzać (im większy bok trójkąta, tym mniejsza długość wysokości). Trójkąt można skonstruować za pomocą konstrukcji geometrycznej, gdzie jest to sposób rysowania figury geometrycznej z wykorzystaniem linijki i cyrkla, gdzie za pomocą linijki wyznaczamy długość odcinków, następnie nanosimy za pomocą cyrkla odległości wierzchołków od narysowanego pierwszego boku, a końcowo łączymy dwa wierzchołki odcinka z punktem przecięcia się okręgów o długości promieni odpowiadającej długości odcinków.

Zadanie 1.
76Zadanie 4.
76Ćwiczenie 1.
78Zadanie 1.
79Zadanie 5.
79Ćwiczenie 1.
81Ćwiczenie 2.
81Ćwiczenie 3.
82Ćwiczenie 5.
83Ćwiczenie 4.
87Zadanie 7.
89Ćwiczenie 2.
91Zadanie 9.
94Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 4.
100Ćwiczenie 2.
102Zadanie 2.
102Ćwiczenie 3.
105Zadanie 3.
106Zadanie 1.
108Zadanie 2.
108Zadanie 12.
109Zadanie 14.
109Pytanie wstępne
73
