W tym zadaniu musisz ocenić, które ze zdań znajdujących się na stronach 101 – 103 są prawdziwe, a które fałszywe.

Prostokąty białe:

1. Liczba –8 to sześcian liczby –2.

Wiadomo, że mnożąc przez siebie nieparzystą ilość liczb ujemnych – wynik będzie zawsze ujemny. Zatem: (–2)³ = –2 ∙ (–2) ∙ (–2) = –8

Zdanie 1 jest prawdziwe.

2. –8,1 to suma liczba 8,7 i . Wykonaj dodawanie.

Zdanie 2 jest nieprawdziwe.

3. 12,5 to różnica liczb i . Wykonaj odejmowanie. Pamiętaj że – i – dają +.

Zdanie 3 jest prawdziwe

4. Liczba 1 jest iloczynem liczb i . Wykonaj mnożenie. Pamiętaj, że mnożąc parzystą ilość liczb ujemnych– wynik będzie zawsze dodatni.

Zdanie 4 jest prawdziwe.

5. Wyrażenie –4² jest równe 16.

Pamiętaj, że + i – dają –. Zatem –4² = –4 ∙ 4 = –16

Zdanie 5 jest nieprawdziwe.

6. to liczba odwrotna do liczby .

Liczby odwrotne to takie, których iloczyn równy jest 1. Aby otrzymać liczbę odwrotną do liczby a, musimy 1 podzielić przez liczbę a. Oznacza to, że liczbę odwracamy „do góry nogami”. Liczby odwrotne mają ten sam znak. Liczba odwrotna do liczby to liczba .

Zdanie 6 jest fałszywe.

7. Liczba –3,12 jest najmniejsza spośród liczb: –3,1; –3,12; 2,58; , –3.109

Jeżeli porównujemy dwie liczby ujemne, to ta z nich jest większa, której wartość bezwzględna jest mniejsza. Z wymienionych liczb najmniejsza jest liczba –3,12.

Zdanie 7 jest prawdziwe.

8. Liczba 8 jest ilorazem liczb –6,4 i –0,8. Wykonaj dzielenie. Wiadomo, że dzieląc liczbę ujemną przez liczbę ujemną– wynik jest zawsze dodatni, ponieważ – i – dają +.

–6,4 : (–0,8) = 8

Zdanie 8 jest prawdziwe.

9. Różnica liczba i jest mniejsza od 0. Wykonaj odejmowanie.

Zdanie 9 jest nieprawdziwe.

10. Liczba 0,1 jest ilorazem liczb 0,8 i 2³. Wykonaj dzielenie.

0,8 : 2³ = 0,8 : 8 = 0,1

Zdanie 10 jest prawdziwe.

11. jest liczbą przeciwną do liczby –3,4.

Liczby do siebie przeciwne, to takie, których suma wynosi 0. Zatem liczba przeciwna do liczby a, to taka, która spełnia równanie a + b = 0. Oznacza to, że liczbą przeciwną do liczby a, jest liczba –a – liczby mają tę samą wartość bezwzględną, ale przeciwny znak.

Liczbą przeciwną do 3,4 jest liczba –3,4.

Zdanie 11 jest prawdziwe.

12. Wartość wyrażenia jest mniejsza od 18. Wykonaj odejmowanie. Pamiętaj, że – i – dają +.

Zdanie 12 jest nieprawdziwe.

13. Suma liczba –14,6; i 16,5 jest mniejsza od zera. Wykonaj dodawanie.

Zdanie 13 jest nieprawdziwe.

14. Liczba jest ilorazem liczb 3 i 2³. Wykonaj dzielenie.

Zdanie 14 jest nieprawdziwe.

15. Liczba 2,5 jest iloczynem liczb –4,5 i . Wiadomo, że mnożąc przez siebie nieparzystą ilość liczb ujemnych – wynik będzie zawsze ujemny.

Zdanie 15 jest nieprawdziwe.

16. Większą wartość bezwzględną od liczby –6,1 ma liczba –6,09. Wartość bezwzględna z liczby a oznaczana jest jako |a|. Wartość bezwzględna liczby dodatniej jest tą samą liczbą dodatnią, czyli |a| = a. Wartość bezwzględna z liczby ujemnej jest liczbą do niej przeciwną, czyli |–a| = a. Wartość bezwzględna z liczby 0 jest równa 0, czyli |0| = 0.

|–6,1|>|–6,09|, ponieważ 6,1 > 6,09

Zdanie 16 jest nieprawdziwe.

17. Liczba –2,6 jest pierwiastkiem równania a : (–0,26) = 10 . Pierwiastkiem równania nazywamy taką liczbę, która spełnia to równanie. Rozwiąż równanie z jedną niewiadomą– oblicz a.

a : (–0,26) = 10 / ∙ (–0,26)

a = 10 ∙ (–0,26)

a = –2,6

Zdanie 17 jest prawdziwe.

18. Wartość wyrażenia –6 : 2 jest mniejsza od –6. Wykonaj dzielenie i porównaj liczby. Jeżeli porównujemy dwie liczby ujemne, to ta z nich jest większa, której wartość bezwzględna jest mniejsza.

–6 : 2 = –3

–3 > –6

Zdanie 18 jest nieprawdziwe.

Prostokąty niebieskie:

1. 15 to liczba biletów o numerach od 50 do 64.

Pierwszy sposób: Wypisz liczby od 50 do 64 i policz je: 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64.

Drugi sposób: Wykonaj odejmowanie: 64 – 50 = 14. Zauważ, że liczba 50 znajduje się w opisanym zbiorze, zatem należy dodać 1 bilet: 14 + 1 = 15.

Zdanie 1 jest prawdziwe

2. Liczba –5 jest mniejsza od –2³.

–2³ = –2 ∙ 2 ∙ 2 = –8

Jeżeli porównujemy dwie liczby ujemne, to ta z nich jest większa, której wartość bezwzględna jest mniejsza.

–8 < –5

Zdanie 2 jest nieprawdziwe.

3. 136 min to czas, który upłynął od 11⁵⁸ do 14¹⁴.

Od 11⁵⁸ do 12⁰⁰ upływają dwie minuty. Od 12⁰⁰ do 14⁰⁰ upływają 2 godziny, czyli 120 minut. Od 14⁰⁰ do 14¹⁴ upływa 14 minut. Zatem: 2 + 120 + 14 = 136 minut.

Zdanie 3 jest prawdziwe.

4. 38 km przejechał rowerzysta, jadąc z 90 min z prędkością 24 .

Prędkość wyrażona jest wzorem , gdzie s oznacza drogę, a t oznacza czas, w jakim przebyta została droga s. Podstaw dane w odpowiednie miejsce i oblicz.

90 min = 1 h 30 min = 1,5 h

Zdanie 4 jest nieprawdziwe.

5. 24 to 15% liczby 160.

Zdanie 5 jest prawdziwe.

6. Liczba 0 jest wartością wyrażenia –4a² + 1 dla a = . Podstaw dane i oblicz.

Zdanie 6 jest prawdziwe.

7. 3600 mm² to pole prostokąta o wymiarach 9 cm x 4 cm.

P = a ∙ b

P = 9 ∙ 4 = 36 cm² = 3600 mm²

Zdanie 7 jest prawdziwe.

8. 16 cm² to pole kwadratu o boku 4 cm oraz rombu o przekątnych 4 cm i 8 cm.

P_k = a²

P_k = 4² = 16 cm²

Zdanie 8 jest prawdziwe.

9. 24 to liczba krawędzi graniastosłupa, którego podstawą jest sześciokąt.

Niech n oznacza liczbę boków wielokąta stanowiącego podstawę graniastosłupa. Graniastosłup ten będzie miał odpowiednio:

– n + 2 ścian,

– 2n wierzchołków,

– 3n krawędzi.

Zatem graniastosłup, który w podstawie ma sześciokąt ma 6 ∙ 3 = 18 krawędzi.

Zdanie 9 jest nieprawdziwe.

10. 42 to liczba, której jest równe 21.

18 ≠ 21

Zdanie 10 jest nieprawdziwe.

11. Kwadrat i romb mają po 4 osie symetrii.

Kwadrat ma 4 osie symetrii, a romb ma 2 osie symetrii.

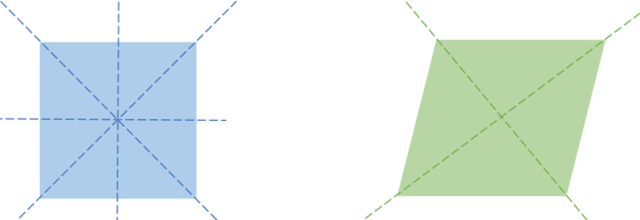
Zdanie 11 jest nieprawdziwe.

12. 73° to miara kąta w trójkącie prostokątnym, w którym drugi kąt ostry jest równy 17°.

Suma miar kątów w trójkącie jest równa 180°. Miara kąta wynosi zatem:

180° – 90° – 17° = 73°

Zdanie 12 jest prawdziwe.

13. 122° to miara kąta rozwartego równoległoboku, w którym kąt ostry jest równy 58°.

Suma miar kątów w równoległoboku jest równa 360°. Miara kąta wynosi zatem:

360° – 58° ∙ 2 = 360° – 116° = 244°

244° : 2 = 122°

Zdanie 13 jest prawdziwe.

14. 96 m² to pole powierzchni całkowitej sześcianu, którego objętość jest równa 64m³.

Objętość sześcianu wyrażona jest wzorem: V = a³, gdzie a oznacza długość boku sześcianu.

64 m³ = a³

a = 4

P_c = 6 ∙ 4²= 6 ∙ 16 = 96m²

Zdanie 14 jest prawdziwe.

15. Deltoid jest trapezem równoramiennym.

Deltoid jest czworokątem, którego przekątne są do siebie prostopadłe oraz jedna z nich jest symetralną drugiej. Deltoid nie jest trapezem równoramiennym.

Zdanie 15 jest nieprawdziwe.

16. 36 to liczby 60 oraz liczby 144.

Zdanie 16 jest prawdziwe.

17. Jedną podstawę ma ostrosłup i stożek.

Zdanie 17 jest prawdziwe.

18. Nie można narysować siatki jednej z brył obrotowych.

Można narysować siatkę stożka i walca, ale nie można narysować siatki kuli.

Zdanie 18 jest prawdziwe.