W tym zadaniu skonstruuj trójkąt równoboczny, okrąg o promieniu równym długości boku trójkąta i styczne w dwóch z wierzchołków trójkąta. Oblicz miarę kąta rozwartego pomiędzy stycznymi.
![]()
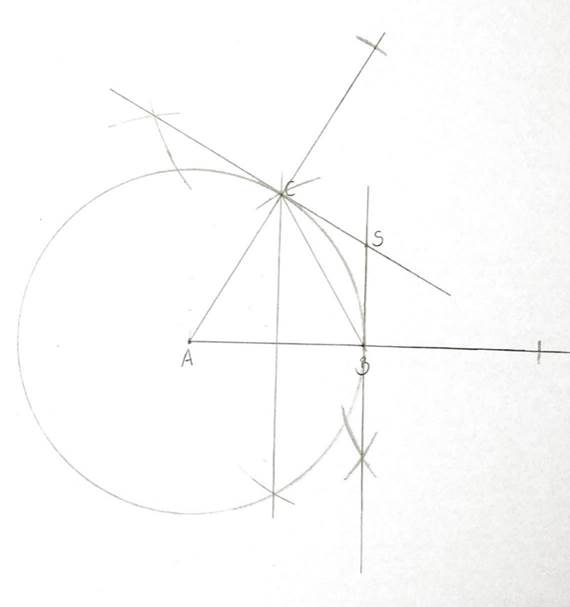

W pierwszej kolejności narysuj odcinek AB i po jednej stronie odcinka z dwóch końców odcinka AB zakreśl dwa łuki o długość odcinka AB tak, by przecięły się w jednym miejscu. Połącz otrzymany punkt odcinkami z punktami A i B. Następnie zakreśl okrąg o środku w punkcie A i promieniu AB. Przedłuż odcinki AC i AB o długość promienia okręgu tak, by punkty C i B były środkami tych odcinków. Następnie znajdź symetralne tych odcinków. Oznacz punkt przecięcia stycznych jako S. W kolejnym kroku oblicz miarę kąta CBS wiedząc, że promień okręgu poprowadzony do punktu styczności stycznej i okręgu jest prostopadły do tej stycznej, a miara kąta wewnętrznego trójkąta równobocznego wynosi
![]() .
.
![]() Na koniec wiedząc, że trójkąt BSC jest równoramienny, oblicz miarę kąta BSC.
Na koniec wiedząc, że trójkąt BSC jest równoramienny, oblicz miarę kąta BSC.
![]()

Zadanie 2.
195Zadanie 3.
195Zadanie 6.
196Zadanie 10.
197Zadanie 11.
197Zadanie 12.
197Zadanie 2.
198Zadanie 3.
198Zadanie 4.
199Zadanie 5.
199Zadanie 6.
199Zadanie 7.
199Zadanie 1.
200Zadanie 2.
201Zadanie 3.
201Zadanie 4.
201Zadanie 5.
201Zadanie 6.
201Zadanie 7.
201Zadanie 8.
201Zadanie 9.
201Zadanie 10.
202Zadanie 11.
202Zadanie 12.
202Zadanie 13.
202Zadanie 14.
202Zadanie 17.
203Zadanie 18.
203Zadanie 20.
203Zadanie 21.*
203Zadanie 22.*
203Zadanie 23.*
204Ćwiczenie 3.
204Zadanie 1.
205Zadanie 2.
205Zadanie 3.
205Zadanie 4.
205Zadanie 5.
205Zadanie 6.
205Zadanie 7.
205Zadanie 8.
205Zadanie 9.
205Zadanie 10.
206Zadanie 11.
206Zadanie 12.
206Zadanie 13.
206Zadanie 14.
207Zadanie 15.
207Zadanie 16.
207Zadanie 18.
207Zadanie 19.
208Zadanie 20.
208Zadanie 22.
208Zadanie 24.
208Zadanie 26.
209Zadanie 30.*
209
