W tym zadaniu musisz udowodnić, że zachodzi
![]() .
.
![]()
![]()
![]()
![]()
Liczba pod pierwiastkiem o stopniu nieparzystym może być liczbą ujemną, tak samo jak wynik tego pierwiastka, dlatego zapisujemy
![]() , więc
, więc
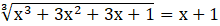 .
.

W tym zadaniu musisz oznaczyć jako lewą część równania
![]() , a jako prawą część równania
, a jako prawą część równania
![]() . Równość jest prawdziwa, gdy lewa strona jest równa prawej stronie. Skorzystaj ze wzoru skróconego mnożenia
. Równość jest prawdziwa, gdy lewa strona jest równa prawej stronie. Skorzystaj ze wzoru skróconego mnożenia
![]() . Pierwiastek sześcienny może być ujemny tak samo jak jego wynik, więc
. Pierwiastek sześcienny może być ujemny tak samo jak jego wynik, więc
![]() .
.

Przykład 1.
55Zadanie 2.
56Zadanie 5.
57Zadanie 6.
57Zadanie 7.
57Zadanie 8.
57Zadanie 9.
57Zadanie 11.
57Zadanie 14.
58Zadanie 15.
58Zadanie 16.
58Zadanie 17.
58Zadanie 18.
59Zadanie 19.
59Przykład 20.
59Zadanie 21.
59Zadanie 22.
59Zadanie 24.
59Ćwiczenie A.
60Ćwiczenie B.
61Przykład 1.
63Przykład 2.
63Przykład 3.
63Przykład 4.
64Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 5.
65Zadanie 6.
65Zadanie 8.
65Zadanie 9.
65Zadanie 10.
65Zadanie 11.
65Zadanie 13.
66Zadanie 14.
66Zadanie 16.
66Zadanie 17.
66Zadanie 18.
66Zadanie 19.
66Zadanie 20.
66Zadanie 21.
67Zadanie 22.
67Ćwiczenie A.
68Przykład 1.
68Przykład 2.
69Przykład 3.
69Zadanie 1.
69Zadanie 2.
70Zadanie 4.
70Zadanie 5.
70Zadanie 6.
70Zadanie 7.
70Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Zadanie 11.
71Ćwiczenie B.
73Ćwiczenie C.
73Przykład 1.
73Przykład 2.
74Zadanie 1.
74Zadanie 2.
74Zadanie 4.
74Zadanie 6.
75Zadanie 7.
75Zadanie 8.
75Zadanie 2.
76Zadanie 4.
76Zadanie 6.
76Zadanie 7.
76Zadanie 8.
76Zadanie 9.
76Zadanie 10.
76Zadanie 12.
76Zadanie 13.
76
