Należy udowodnić podane twierdzenie.
Gdy a i b są liczbami naturalnymi ≠ 0 oraz x ≠ 0, to:
xa : xb = (x · x · … · x) : (x · … · x ) = (x · x · … · x) / (x · … · x ) = (x · … · x) = xa – b
Gdy a = 0, x ≠ 0, m to dowolna liczba całkowita ≠ 0, to:
xa : xb = 1 : xb = x0 – b = xa – b, dla b = 0 zachodzi to samo, jak również dla a = 0 i b = 0
Gdy a i b są ujemne i całkowite, to można zapisać a = -n i b = -m, gdzie n i m są naturalne dodatnie, x ≠ 0, więc:
![]()
Gdy a ≥ 0, b < 0 lub a < 0 i b ≥ 0, to:
b = -m, gdzie m naturalna dodatnia
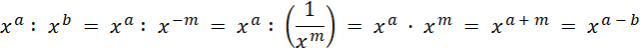

Rozpatrz wszystkie przypadki i doprowadź do poszukiwanej postaci.

Ćwiczenie 1.
115Ćwiczenie 2.
116Ćwiczenie 3.
117Ćwiczenie 4.
118Zadanie 1.
119Zadanie 2.
119Zadanie 3.
119Zadanie 7.
120Zadanie 8.
120Zadanie 9.
120Zadanie 12.
120Zadanie 13.
120Ćwiczenie 1.
123Ćwiczenie 2.
123Ćwiczenie 3.
124Ćwiczenie 4.
125Ćwiczenie 5.
125Ćwiczenie 7.
127Zadanie 1.
128Zadanie 3.
128Zadanie 4.
128Zadanie 6.
128Zadanie 7.
128Zadanie 8.
128Zadanie 10.
129Zadanie 11.
129Zadanie 12.
129Zadanie 13.
129Zadanie 14.
129Zadanie 15.
129Zadanie 17.
129Ćwiczenie 1.
148Ćwiczenie 2.
148Ćwiczenie 3.
150Ćwiczenie 4.
150Ćwiczenie 5.
150Zadanie 1.
152Zadanie 2.
152Zadanie 3.
152Zadanie 4.
152Zadanie 5.
152Zadanie 6.
153Zadanie 8.
153Zadanie 10.
153Zadanie 11.
153Zadanie 14.
154Zadanie 16.
154Zadanie 17.
154Zadanie 18.
154Zadanie 19.
154Zadanie zestaw 3 9.
182
