Narysuj wykresy dwóch podanych prostych i wskaż punkt, w których wykresy się przetną.
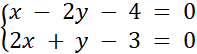
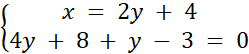
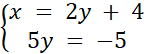
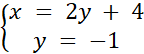
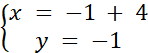
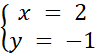
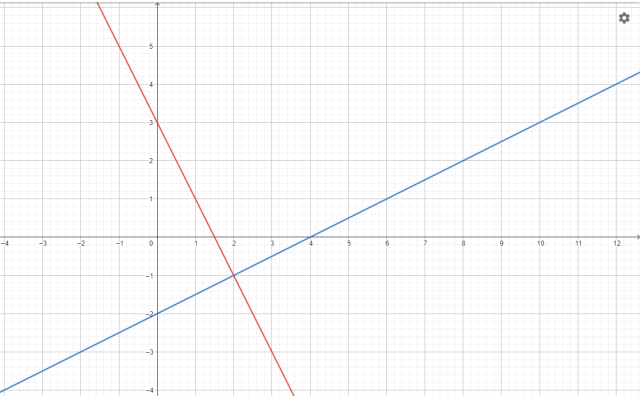

Znaleziono rozwiązanie podanego układu równań. Metoda przeciwnych współczynników polega odpowiednim przemnożeniu obu stron danego równania tak, aby po zsumowaniu obydwu równań, wyrażenia podobne się uprościły. Metoda podstawienia polega na zapisaniu jednej zmiennej w postaci wyrażenia zawierającego drugą zmienną (np. y = 2x – 2), a następnie wstawieniu tego wyrażenia do drugiego równania, w miejsce zmiennej. Aby sprawdzić poprawność obliczeń narysowano w układzie współrzędnych obu prostych i wyznaczano punkt ich przecięcia. Współrzędne punkty przecięcia osi odpowiadają wynikowi układu równań.

Zadanie 1.1.
306Zadanie 1.2.
306Zadanie 1.3.
306Zadanie 1.4.
306Zadanie 1.5.
307Zadanie 1.6.
307Zadanie 1.7.
307Zadanie 1.8.
307Zadanie 1.9.
307Zadanie 1.10.
307Zadanie 2.1.
314Zadanie 2.2.
314Zadanie 2.3.
315Zadanie 2.4.
315Zadanie 2.5.
315Zadanie 2.6.
315Zadanie 2.7.
315Zadanie 2.12.
315Zadanie 2.13.
316Zadanie 2.15.
316Zadanie 2.17.
316Zadanie 2.20.
316Zadanie 5.
317Zadanie 6.
317Zadanie 3.1.
322Zadanie 3.2.
323Zadanie 3.3.
323Zadanie 3.4.
323Zadanie 3.6.
323Zadanie 3.7.
324Zadanie 3.8.
324Zadanie 3.12.
324Zadanie 4.1.
329Zadanie 4.2.
329Zadanie 4.3.
329Zadanie 4.4.
330Zadanie 4.5.
330Zadanie 4.6.
330Zadanie 4.7.
330Zadanie 4.8.
331Zadanie 4.14.
332Zadanie 5.2.
339Zadanie 5.3.
339Zadanie 5.4.
339Zadanie 5.5
340Zadanie 5.6
340Zadanie 5.7.
340Zadanie 5.9.
340Zadanie 5.10.
340Zadanie 5.11.
340Zadanie 5.12.
340Zadanie 5.13.
341Zadanie 5.14.
341Zadanie 5.15.
341Zadanie 5.16.
341Zadanie 5.17.
341Zadanie 5.18.
341Zadanie 5.19.
341Zadanie 5.20.
341Zadanie 6.3.
346Zadanie 6.5.
347Zadanie 6.6..
347Zadanie 7.2.
352Zadanie 7.3.
353Zadanie 7.4
353Zadanie 7.5.
353Zadanie 7.9.
354Zadanie 32.
360Zadanie 36.
360Zadanie 37.
360Zadanie 38.
360Zadanie 39.
361Zadanie 40.
361Zadanie 41.
361Zadanie 45.
361Zadanie 50.
362Zadanie 51.
362Zadanie 52.
362
