Podaj przykład narysowanych funkcji. Rozwiązaniem układu jest punkt, w którym obie funkcje się przecinają.
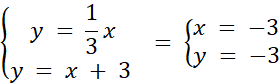

Punkty przecięcia wykresu funkcji z osią OY, obliczamy przez wstawienia za x zera i wyliczenie y lub f(x).

Zadanie 1.1.
306Zadanie 1.2.
306Zadanie 1.3.
306Zadanie 1.4.
306Zadanie 1.5.
307Zadanie 1.6.
307Zadanie 1.7.
307Zadanie 1.8.
307Zadanie 1.9.
307Zadanie 1.10.
307Zadanie 2.1.
314Zadanie 2.2.
314Zadanie 2.3.
315Zadanie 2.4.
315Zadanie 2.5.
315Zadanie 2.6.
315Zadanie 2.7.
315Zadanie 2.12.
315Zadanie 2.13.
316Zadanie 2.15.
316Zadanie 2.17.
316Zadanie 2.20.
316Zadanie 5.
317Zadanie 6.
317Zadanie 3.1.
322Zadanie 3.2.
323Zadanie 3.3.
323Zadanie 3.4.
323Zadanie 3.6.
323Zadanie 3.7.
324Zadanie 3.8.
324Zadanie 3.12.
324Zadanie 4.1.
329Zadanie 4.2.
329Zadanie 4.3.
329Zadanie 4.4.
330Zadanie 4.5.
330Zadanie 4.6.
330Zadanie 4.7.
330Zadanie 4.8.
331Zadanie 4.14.
332Zadanie 5.2.
339Zadanie 5.3.
339Zadanie 5.4.
339Zadanie 5.5
340Zadanie 5.6
340Zadanie 5.7.
340Zadanie 5.9.
340Zadanie 5.10.
340Zadanie 5.11.
340Zadanie 5.12.
340Zadanie 5.13.
341Zadanie 5.14.
341Zadanie 5.15.
341Zadanie 5.16.
341Zadanie 5.17.
341Zadanie 5.18.
341Zadanie 5.19.
341Zadanie 5.20.
341Zadanie 6.3.
346Zadanie 6.5.
347Zadanie 6.6..
347Zadanie 7.2.
352Zadanie 7.3.
353Zadanie 7.4
353Zadanie 7.5.
353Zadanie 7.9.
354Zadanie 32.
360Zadanie 36.
360Zadanie 37.
360Zadanie 38.
360Zadanie 39.
361Zadanie 40.
361Zadanie 41.
361Zadanie 45.
361Zadanie 50.
362Zadanie 51.
362Zadanie 52.
362
