Wyznacz grubość blachy, gdy jego gęstość jest równa gęstości wody.
DANE:
a = 10 cm
![]()
![]()
SZUKANE:
b = ?
WZÓR:
![]()
ms =
![]() ∙ [a3 – (a – 2 ∙ b)3]
∙ [a3 – (a – 2 ∙ b)3]
V1 = a3
V2 = c3 = (a – 2 ∙ b)3
c = a – b – b = a – 2 ∙ b
Vs = V1 – V2 = a3 – (a – 2 ∙ b)3
![]() | ∙ a3
| ∙ a3
![]()
![]() = a3 – (a – 2 ∙ b)3
= a3 – (a – 2 ∙ b)3
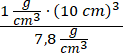 = (10 cm)3 – (10 cm – 2b)3
= (10 cm)3 – (10 cm – 2b)3
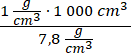 = 1 000 cm3 – (10 cm – 2b)3
= 1 000 cm3 – (10 cm – 2b)3
128,21 cm3 = 1 000 cm3 – (10 cm – 2b)3
(10 cm – 2b)3 = 1 000 cm3 – 128,21 cm3
(10 cm – 2b)3 = 871,79 cm3 |
![]()
![]()
10 cm – 2b ≈ 9,55 cm
2b ≈ 10 cm – 9,55 cm
2b ≈ 0,45 cm | : 2
b ≈ 0,225 cm

Objętość sześcianu wyrażana jest jako: x3, gdzie x – długość jego krawędzi.
Gęstość całego sześcianu to stosunek całej masy stali użytej do jego zbudowania oraz objętości, jaką zajmuje. Z zadania wiemy, że jest równa gęstości wody.
Jego objętość można policzyć jako różnicę objętości dwóch sześcianów. Pierwszy to, gdyby cały sześcian był pełny (V1), a drugi to sześcian wewnętrzny (V2), pomniejszony o dwie grubości blachy. Masa użytej stali to iloczyn jej gęstości (
![]() ) oraz objętości (Vs).
) oraz objętości (Vs).
Dokonując przekształceń, wyznaczam szukaną grubość blachy (b).

Zadanie 31.5.
114Zadanie 31.11.
115Zadanie 31.12.
115Zadanie 31.13.
116Zadanie 32.9.
118Zadanie 32.13.
119Zadanie 32.14.
119Zadanie 32.15.
119Zadanie 33.3.
120Zadanie 33.7.
121Zadanie 33.9.
121Zadanie 33.12.
121Zadanie 33.13.
121Zadanie 34.1.
122Zadanie 34.8.
123Zadanie 34.14.
123Zadanie 34.19.
124Zadanie 34.21.
125Zadanie 34.22.
125Zadanie 34.26.
125Zadanie 34.28.
126Zadanie 35.4.
127Zadanie 35.9.
127Zadanie 35.10.
127Zadanie 35.11.
128Zadanie 35.12.
128Zadanie 36.7.
130Zadanie 36.12.
130Zadanie 36.14.
130Zadanie 36.22.
131Zadanie 36.23.
131Zadanie 36.24.
132Zadanie 36.25.
132Zadanie 36.31.
133Zadanie 36.35.
133
