Jeśli kąt padania wynosi
![]() , to również promień odbity będzie nachylony pod tym kątem. Kąt między promieniem odbitym i padającym wyniesie
, to również promień odbity będzie nachylony pod tym kątem. Kąt między promieniem odbitym i padającym wyniesie
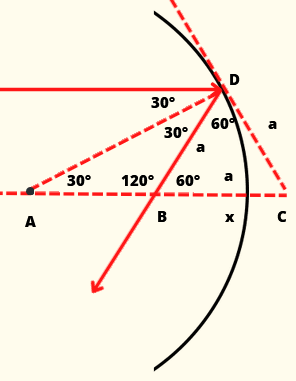
![]() . Od punktu odbicia prowadzimy przerywane linie do punktu A. Odległości między A i dowolnym punktem zwierciadła to jego promień R. Prowadząc przerywaną linię dalej (do punktu C; normalna) utworzymy trójkąt prostokątny. Z tegoż warunku mamy kąt między
. Od punktu odbicia prowadzimy przerywane linie do punktu A. Odległości między A i dowolnym punktem zwierciadła to jego promień R. Prowadząc przerywaną linię dalej (do punktu C; normalna) utworzymy trójkąt prostokątny. Z tegoż warunku mamy kąt między
![]() równy 60 stopni. Promień padający jest równoległy do osi optycznej, więc kąt między promieniem padającym i odbitym będzie równy kątowi miedzy
równy 60 stopni. Promień padający jest równoległy do osi optycznej, więc kąt między promieniem padającym i odbitym będzie równy kątowi miedzy
![]() . Otrzymujemy trójkąt równoboczny o boku a. Stąd pierwsze równanie:
. Otrzymujemy trójkąt równoboczny o boku a. Stąd pierwsze równanie:
![]()
Z drugiej strony mamy trójkąt
![]() , gdzie kąt dopełniający do prostej (osi optycznej) wynosi oczywiście 120 stopni, gdyż:
, gdzie kąt dopełniający do prostej (osi optycznej) wynosi oczywiście 120 stopni, gdyż:
![]()
Wiemy, iż suma kątów w dowolnym trójkącie wynosi 180 stopni, więc:
![]()
Stąd otrzymujemy kąt nachylenia odcinka
![]() do osi optycznej:
do osi optycznej:
![]()
Można było to wykazać z podobieństw trójkątów. Skoro bok
![]() ma długość a oraz trójkąt rozwartokątny
ma długość a oraz trójkąt rozwartokątny
![]() ma takie same kąty przy podstawie, to jest on trójkątem równoramiennym o podstawie R i bokach równych a. Konstruujemy stąd układ trzech równań:
ma takie same kąty przy podstawie, to jest on trójkątem równoramiennym o podstawie R i bokach równych a. Konstruujemy stąd układ trzech równań:
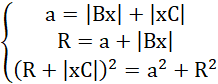
Ostatnie równanie jest wykorzystaniem twierdzenia Pitagorasa do trójkąta prostokątnego
![]() . Podstawiamy za R w trzecim równaniu drugie równanie:
. Podstawiamy za R w trzecim równaniu drugie równanie:
![]()
Z pierwszego równania zamieniamy
![]() na a:
na a:
![]()
![]()
![]()
Po spierwiastkowaniu otrzymamy:
![]()
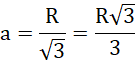
Na koniec podstawiamy to do równania drugiego:
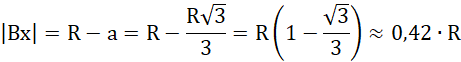

Rozwiązując zadanie, pamiętaj o wykorzystaniu prawa odbicia. Musisz zauważyć związki geometryczne, które są widoczne w tym układzie (trójkąt BCD jest równoboczny, co oznacza, iż kąty wewnętrzne wynoszą
![]() ).
).