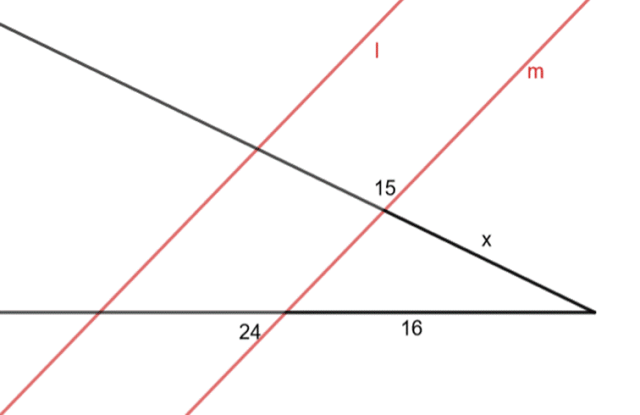
Oblicz długości odcinków
i
przedstawionych na rysunku, jeśli proste
i
są równoległe.
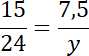
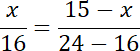
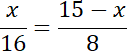
Zauważ, że możesz skorzystać z twierdzenia Talesa mówiącego o tym, że jeśli ramiona kąta są przecięte dwoma prostymi równoległymi, to długości odcinków wyznaczonych przez te proste na jednym ramieniu tego kąta są proporcjonalne do długości odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu. Rysunek podany w treści zadania przedstaw w takiej postaci, aby można było skorzystać z powyższego twierdzenia.
Na tej podstawie zapisz proporcję z boków zawartych pomiędzy prostymi
i
, a następnie pomiędzy prostymi
i
. Podstaw ich długości, powstałe równania wymnóż na skos i wyznacz z nich wartości
i
.