| Wzór funkcji |
|
|
|
|
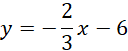
| Punkt przecięcia wykresu z osią y | (0,-6) | (0,3) | (0,-10) | (0,7) |
| Punkt przecięcia wykresu z osią x | (-9,0) | (-2,0) | (1,0) | Nie ma |
| Miejsce zerowe funkcji | x = -9 | x = -2 | x = 1 | Nie ma |
Wartość funkcji dla
|
| 4,5 | 0 | y = 7 |
Argumenty, dla których
|
|
|
|
|
| Ćwiartki układu współrzędnych przecinane przez wykres | II, III, IV | I, II, III | I, III, IV | I, II |
Wzór ogólny funkcji liniowej to
. Punkt przecięcia z osią y obliczasz dla x = 0.
Punkt przecięcia z osią y jest określony przez wyraz wolny.
Miejsce zerowe funkcji to taki argument, dla którego funkcja ma wartość 0 – znajdując x, możesz określić również punkt przecięcia z osią x. Argumenty, dla których
określisz na podstawie miejsca zerowego oraz współczynnika kierunkowego prostej – czy funkcja jest rosnąca (a>0) czy malejąca (a<0).
Ćwiartki układu współrzędnych numeruje się, zaczynając od prawej górnej, przeciwnie do ruchu wskazówek zegara:
W I ćwiartce x > 0 i y > 0
W II ćwiartce x < 0 i y > 0
W III ćwiartce x < 0 i y < 0
W IV ćwiartce x > 0 i y < 0
Uzupełnij tabelę, korzystając z powyższych informacji. Kolumna 1.
Wzór funkcji:
Punkt przecięcia z osią y
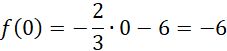
Miejsce zerowe i punkt przecięcia z osią x
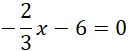
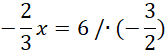
Wartość funkcji dla x = 1
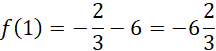
Jeśli funkcja jest malejąca i przecina oś y, poniżej 0 to znaczy, że przechodzi przez ćwiartki II, III i IV.
Kolumna 2. Na podstawie punktów przecięcia z osiami wyznacz wzór funkcji
Wzór funkcji:
Wartość funkcji dla x = 1
Argumenty, dla których funkcja przyjmuje wartości dodatnie, jeśli jest rosnąca i miejsce zerowe x = -2
dla
Jeśli funkcja jest rosnąca i przecina oś y powyżej 0, to znaczy, że przechodzi przez ćwiartki I, II i III.
Kolumna 3. Na podstawie punktów przecięcia z osiami wyznacz wzór funkcji
Wzór funkcji:
Wartość funkcji dla x = 1
Argumenty, dla których funkcja przyjmuje wartości dodatnie, jeśli jest rosnąca i miejsce zerowe x = 1
dla
Jeśli funkcja jest rosnąca i przecina oś y poniżej 0, to znaczy, że przechodzi przez ćwiartki I, III i IV.
Kolumna 4. Jeżeli funkcja nie przecina osi x w żadnym punkcie (nie ma miejsca zerowego) to znaczy, że jest stała. Dla każdego x,
.
Jeśli funkcja jest stała i ma wartość dodatnią, to znaczy, że przechodzi przez ćwiartki I i II.