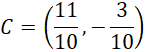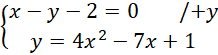
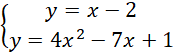
![]()
![]()
![]()
![]()
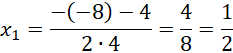
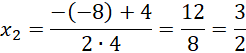
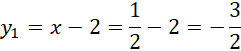
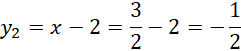
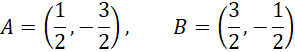
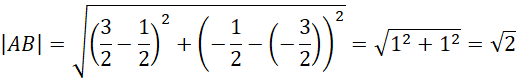
Trójkąt ABC jest prostokątny, kąt ACB jest prosty.
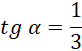
![]()
![]()
![]()
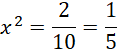
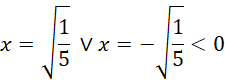
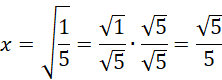
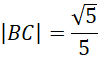
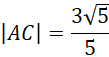
![]()
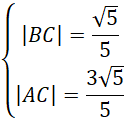
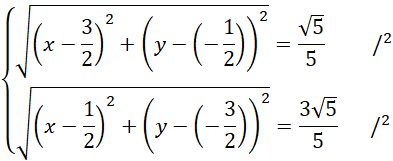
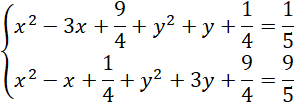
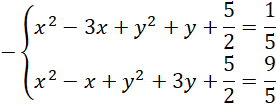
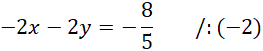
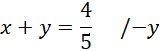
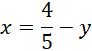
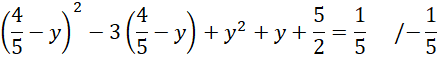
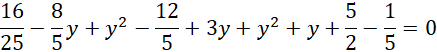
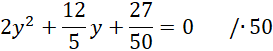
![]()
![]()
![]()
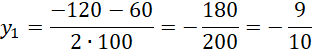
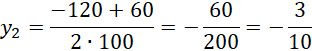
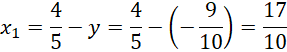
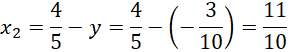
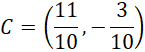
ODP: Punkt
![]() ma współrzędne
ma współrzędne
![]()

Oblicz współrzędne przecięcia prostej
![]() i paraboli, czyli współrzędne punktów A i B. Zrobisz to rozwiązując układ dwóch równań będącymi wzorami obu tych funkcji.
i paraboli, czyli współrzędne punktów A i B. Zrobisz to rozwiązując układ dwóch równań będącymi wzorami obu tych funkcji.
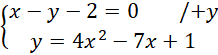
Z pierwszego równania wyznacz wartość
![]() .
.
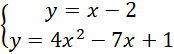
Porównaj ze sobą wartości
![]() w obu równaniach.
w obu równaniach.
![]()
Przenieś wszystkie wartości na prawą stronę równania.
![]()
Oblicz deltę i miejsca zerowe powstałego równania.
![]()
![]()
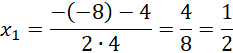
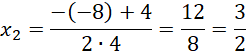
Zauważ, że znasz pierwsze współrzędne obu punktów, na tej podstawie oblicz ich drugą współrzędną.
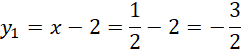
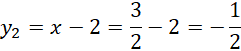
Zapisz współrzędne punktów A i B.
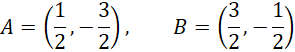
Oblicz długość odcinka AB, czyli średnicę okręgu o środku O.
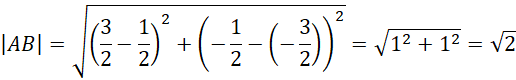
Zauważ, że trójkąt ABC jest prostokątny, kąt ACB jest prosty, ponieważ jest to kąt wpisany oparty na tym samym łuku, co średnica okręgu, więc jego miara jest dwa razy mniejsza od kąta AOB
![]()
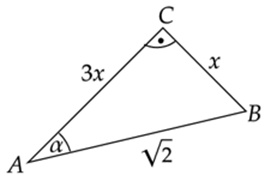
Wykonaj rysunek pomocniczy trójkąta ABC. Skorzystaj z własności funkcji trygonometrycznych w trójkącie prostokątnym oraz tego, że
![]()
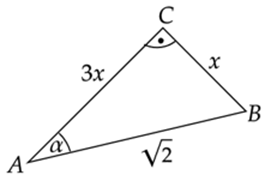
Skorzystaj z twierdzenia Pitagorasa w trójkącie ABC i oblicz wartość
![]() .
.
![]()
![]()
![]()
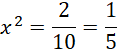
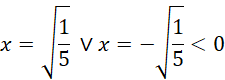
Długość boku musi być dodatnia. Usuń niewymierność z mianownika, czyli pomnóż licznik i mianownik ułamka przez
![]() .
.
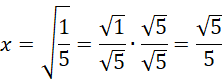
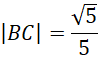
Znasz już długość odcinka BC, na tej podstawie oblicz długość odcinka AC.
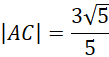
Pozostało obliczyć współrzędne punktu C. Oznacz go jako:
![]()
Zauważ, że znasz długości odcinków AC i BC.
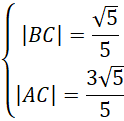
Zapisz wzór na długości powyższych odcinków. Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Podnieś każde z nich obustronnie do kwadratu i skorzystaj ze wzorów skróconego mnożenia na kwadrat różnicy:
![]() oraz kwadrat sumy:
oraz kwadrat sumy:
![]()
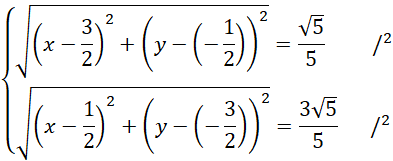
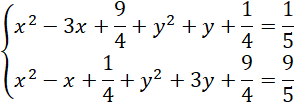
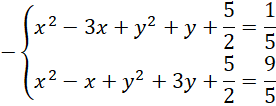
Odejmij obustronnie oba równania.
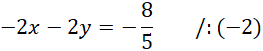
Z powstałego równania wyznacz wartość
![]()
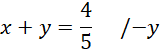
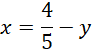
Podstaw obliczoną wartość
![]() pod jedno z równań znajdujących się w układzie równań. Wymnóż nawiasy, przenieś wszystkie wartości na lewą stronę równania i dokonaj redukcji jednomianów podobnych.
pod jedno z równań znajdujących się w układzie równań. Wymnóż nawiasy, przenieś wszystkie wartości na lewą stronę równania i dokonaj redukcji jednomianów podobnych.
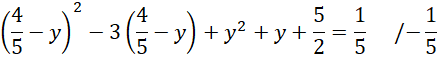
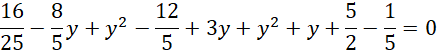
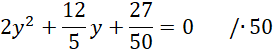
![]()
Zauważ, że powstało równanie kwadratowe. Oblicz deltę i miejsca zerowe, aby obliczyć jego rozwiązanie.
![]()
![]()
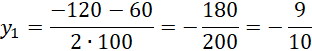
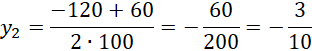
Oblicz współrzędne
![]() . Skorzystaj z tego, że
. Skorzystaj z tego, że
![]()
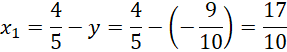
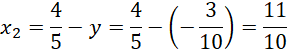
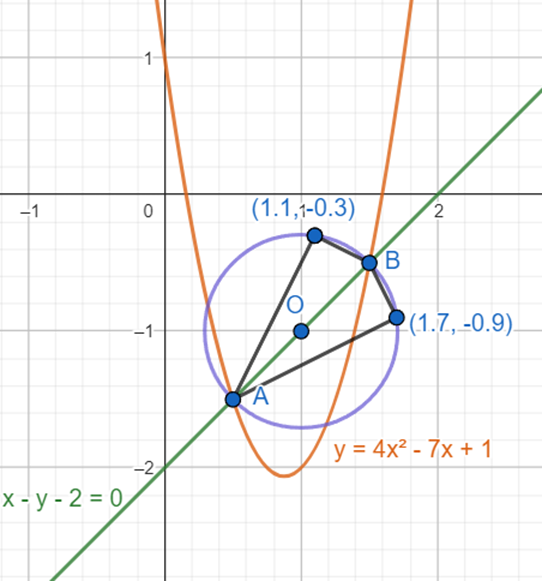
Zaznacz obliczone współrzędne punktów na rysunku.
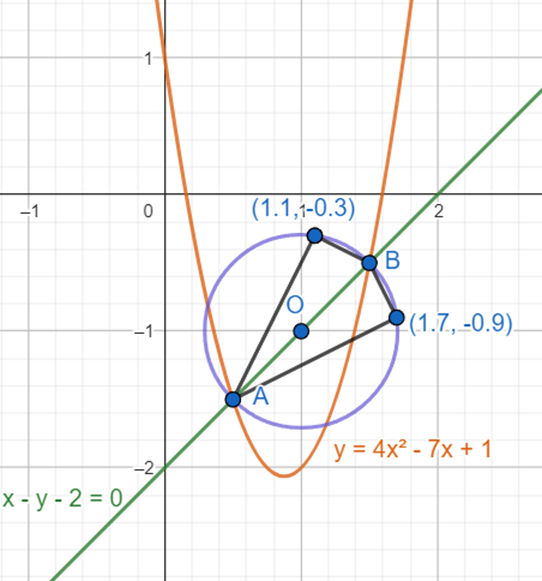
Z treści zadania wiesz, że punkt C ma znajdować się nad prostą
![]() . Na tej podstawie zapisz jego współrzędne.
. Na tej podstawie zapisz jego współrzędne.