![]()
![]()
![]()
Trójkąty ABC, ABD i BCD to trójkąty szczególne. Ich miary kątów to
![]() .
.
W trójkącie ABD:
![]()
![]()
W trójkącie ABC:
![]()
![]()
![]()
Trójkąt KBL jest równoramienny prostokątny, więc jego miary kątów to
![]() – trójkąt szczególny.
– trójkąt szczególny.
![]()
![]()
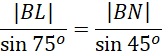
![]()
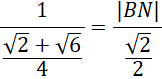
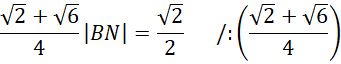
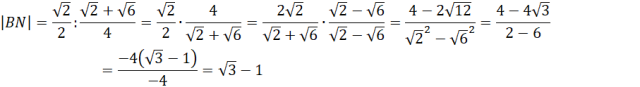
![]()
To kończy dowód.

Oblicz brakujące miary kątów w trójkątach ABD, ACB i CBD. Zauważ, że każdy z nich jest prostokątny.
![]()
![]()
![]()
Trójkąty ABC, ABD i BCD to trójkąty szczególne. Ich miary kątów to
![]() . Oznacza to, że długość boku znajdującego się naprzeciwko średniego kąta jest o
. Oznacza to, że długość boku znajdującego się naprzeciwko średniego kąta jest o
![]() razy większa od długości boku znajdującego się naprzeciwko najmniejszego kąta, a długość boku znajdującego się naprzeciwko największego kąta jest 2 razy większa od długości najkrótszego boku. Na tej podstawie zapisz długości boków w tych trójkątach.
razy większa od długości boku znajdującego się naprzeciwko najmniejszego kąta, a długość boku znajdującego się naprzeciwko największego kąta jest 2 razy większa od długości najkrótszego boku. Na tej podstawie zapisz długości boków w tych trójkątach.
W trójkącie ABD:
![]()
![]()
W trójkącie ABC:
![]()
![]()
Więc:
![]()
Zauważ, że trójkąt KBL jest równoramienny prostokątny, jego miary kątów to
![]() , więc jest to trójkąt szczególny. Oznacza to, że długość boku znajdującego się naprzeciwko kąta prostego jest o
, więc jest to trójkąt szczególny. Oznacza to, że długość boku znajdującego się naprzeciwko kąta prostego jest o
![]() razy większa od długości każdego z jego ramion. Na tej podstawie zapisz miarę brakującego boku w trójkącie KBL.
razy większa od długości każdego z jego ramion. Na tej podstawie zapisz miarę brakującego boku w trójkącie KBL.
![]()
Oblicz brakującą miarę kąta w trójkącie BNL.
![]()
Skorzystaj z twierdzenia sinusów w trójkącie BNL.
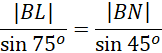
Oblicz wartość
![]() Skorzystaj ze wzoru na sumę kątów w sinusie oraz wartości funkcji trygonometrycznych dla wybranych kątów.
Skorzystaj ze wzoru na sumę kątów w sinusie oraz wartości funkcji trygonometrycznych dla wybranych kątów.
![]()
Podstaw znane wartości do zapisanego powyżej twierdzenia sinusów.
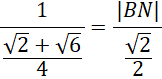
Pomnóż na skos i z powstałego równania oblicz długość boku BN.
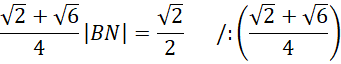
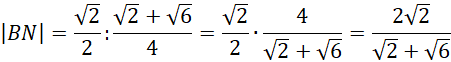
Pamiętaj o usunięciu niewymierności z mianownika, czyli pomnożeniu licznika i mianownika ułamka przez wartość znajdującą się w mianowniku z przeciwnym znakiem pomiędzy pierwiastkami.
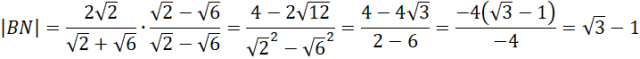
Pozostało obliczyć długość odcinka ND. Zauważ, że zrobisz to odejmując od długości boku BD obliczoną powyżej długość odcinka BN.
![]()
To kończy dowód.