![]()
![]()
![]()
![]()
![]()
![]()

Symbol większości i mniejszości: > i < oznacza, że tego elementu nie zaliczamy do zbioru. Na osi oznaczamy go pustą kropką i przedziałem „na skos”, przedział przy tym elemencie zapisujemy używając nawiasu okrągłego ( ) i mówimy, że przedział jest otwarty, lub otwarty prawo/lewostronnie.
Symbol większe lub równe, mniejsze lub równe:
![]() oznacza, że ten element zalicza się do zbioru. Na osi oznaczamy go zaczernionym punktem i przedziałem pionowym do góry, przedział przy tym elemencie zapisujemy, używając nawiasu ostrego
oznacza, że ten element zalicza się do zbioru. Na osi oznaczamy go zaczernionym punktem i przedziałem pionowym do góry, przedział przy tym elemencie zapisujemy, używając nawiasu ostrego
![]() i mówimy, że przedział jest domknięty, lub domknięty prawo/lewostronnie.
i mówimy, że przedział jest domknięty, lub domknięty prawo/lewostronnie.
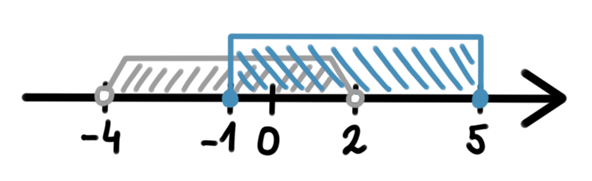
Zaznacz na osiach odpowiednie przedziały, zwracając uwagę na to, jaki nawias został użyty. Następnie w tym podpunkcie musisz wypisać przedziały, które są różnicą pierwszego i drugiego przedziału:
![]() – przedział jest prawostronnie otwarty, ponieważ -1 należy do przedziału B, czyli nie może znaleźć się w wyniku.
– przedział jest prawostronnie otwarty, ponieważ -1 należy do przedziału B, czyli nie może znaleźć się w wyniku.
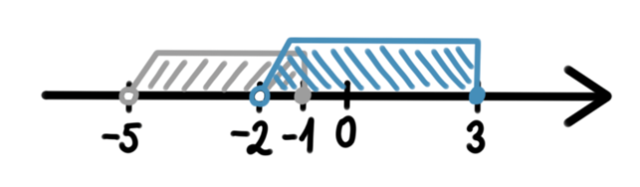
![]() – przedział jest prawostronnie domknięty, ponieważ -2 nie należy do przedziału D, czyli nie jest odejmowane, znajduje się w wyniku.
– przedział jest prawostronnie domknięty, ponieważ -2 nie należy do przedziału D, czyli nie jest odejmowane, znajduje się w wyniku.
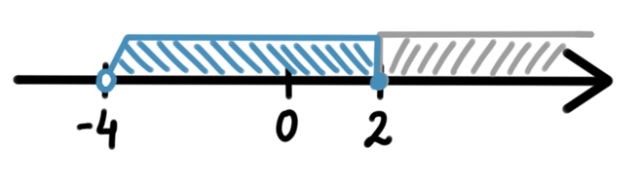
![]() – przedział jest lewostronnie otwarty, ponieważ 2 należy do przedziału F, czyli nie może znaleźć się w wyniku, bo zostało odjęte.
– przedział jest lewostronnie otwarty, ponieważ 2 należy do przedziału F, czyli nie może znaleźć się w wyniku, bo zostało odjęte.
Uważaj na nawias przy znaku nieskończoności – w tym przypadku zawsze używa się nawiasu okrągłego. W ćwiczeniach prawdopodobnie znajduje się błąd.