Oblicz długość najkrótszej wysokości trójkąta, który ma boki o długościach 7, 15 i 16.

Z tw. Pitagorasa w ABC
![]()
![]()
Z tw. Pitagorasa w BCD
![]()
![]()
![]()
![]()
![]()
49 = 225 – 256 + 32a
49 = -31 + 32a
80 = 32a
a = 2,5
![]()
![]()
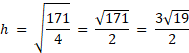

Najkrótsza wysokość będzie opuszczona na najdłuższy bok, czyli bok o długości 16. Niech spodek wysokości h dzieli bok o długości 16 na dwa odcinki o długościach a i 16 – a. Wylicz
![]() korzystając z twierdzenia Pitagorasa w trójkącie ABC. Następnie wylicz
korzystając z twierdzenia Pitagorasa w trójkącie ABC. Następnie wylicz
![]() korzystając z twierdzenia Pitagorasa w trójkącie BCD. Kolejno przyrównaj do siebie obie wyliczone wartości
korzystając z twierdzenia Pitagorasa w trójkącie BCD. Kolejno przyrównaj do siebie obie wyliczone wartości
![]() , aby wyznaczyć wartość a. Znając wartość a, oblicz wartość h.
, aby wyznaczyć wartość a. Znając wartość a, oblicz wartość h.

Zadanie 2.
119Zadanie 3.
119Zadanie 10.
120Zadanie 4.
121Zadanie 6.
122Zadanie 7.
122Zadanie 11.
122Zadanie 17.
123Zadanie 18.
123Zadanie 4.
124Zadanie 8.
125Zadanie 13.
125Zadanie 1.
127Zadanie 2.
127Zadanie 4.
127Zadanie 8.
128Zadanie 11.
128Zadanie 15.
128Zadanie 19.
129Zadanie 1.
130Zadanie 2.
130Zadanie 3.
130Zadanie 5.
130Zadanie 7.
130Zadanie 8.
131Zadanie 9.
131Zadanie 10.
131Zadanie 11.
131Zadanie 15.
131Zadanie 18.
132Zadanie 19.
132Zadanie 22.
132Zadanie 23.
132Zadanie 1.
133Zadanie 2.
133Zadanie 3.
133Zadanie 4.
133Zadanie 5.
133Zadanie 6.
133Zadanie 7.
134Zadanie 8.
134Zadanie 10.
134Zadanie 11.
134Zadanie 13.
134Zadanie 14.
134Zadanie 24.
135Zadanie 25.
135Zadanie 1.
136Zadanie 2.
136Zadanie 3.
136Zadanie 4.
136Zadanie 5.
136Zadanie 6.
136Zadanie 7.
137Zadanie 9.
137Zadanie 10.
137Zadanie 13.
137Zadanie 16.
137Zadanie 18.
138Zadanie 20.
138Zadanie 21.
138Zadanie 23.
138Zadanie 25.
138Zadanie 1.
139Zadanie 2.
139Zadanie 6.
139Zadanie 7.
139Zadanie 8.
140Zadanie 14.
140Zadanie 15.
140Zadanie 17.
141Zadanie 3.
142Zadanie 4.
142Zadanie 5.
142Zadanie 7.
142Zadanie 8.
143Zadanie 10.
143Zadanie 11.
143Zadanie 13.
143Zadanie 14.
143Zadanie 15.
143Zadanie 21.
144Zadanie 9.
146Zadanie 19.
147Zadanie 20.
147Zadanie 21.
147Zadanie 22.
147Zadanie 23.
147Zadanie 24.
147Zadanie 25.
147Zadanie 27.
147Zadanie 29.
148Zadanie 31.
148
