W tym zadaniu podaj czas, po jakim liczba bakterii zwiększyła się dwukrotnie w porównaniu do początkowego stanu, jeśli po dwóch godzinach od początku zwiększyła się trzykrotnie. Przyjmij, że tempo wzoru liczebności bakterii jest stałe, a 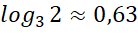
![]()
2a – liczba bakterii po szukanym czasie t
![]()
![]()
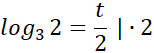
![]()
1,26 h = 75, 6 min = 1 h 16 min
Odp.: Liczba bakterii zwiększyła się dwukrotnie po 1 h 16 min.

Aby rozwiązać to zadanie opisz przyrost liczebności bakterii jako funkcję czasu. Następnie korzystając z podanych informacji wyznacz czas po jakim ilość bakterii będzie dwa razy taka jak początkowa ilość.

Zadanie 1.1.
278Zadanie 1.2.
278Zadanie 1.3.
278Zadanie 1.4.
278Zadanie 1.5.
278Zadanie 1.6.
278Zadanie 1.7.
279Zadanie 1.8.
279Zadanie 1.9.
279Zadanie 1.11.
279Zadanie 2.1.
286Zadanie 2.2.
278Zadanie 2.3.
286Zadanie 2.4.
286Zadanie 2.9.
286Zadanie 2.10.
287Zadanie 2.11.
287Zadanie 2.12.
287Zadanie 2.13.
287Zadanie 2.14.
287Zadanie Prosto do matury 7.
288Zadanie 3.1.
291Zadanie 3.2.
291Zadanie 3.3.
291Zadanie 3.4.
291Zadanie 3.5.
291Zadanie 4.1.
296Zadanie 4.2.
297Zadanie 4.3.
297Zadanie 4.4.
297Zadanie 4.5.
297Zadanie 4.6.
297Zadanie 4.7.
297Zadanie 4.8.
298Zadanie 4.9.
298Zadanie 4.10.
298Zadanie 4.11.
298Zadanie 4.14.
298Zadanie 5.1.
306Zadanie 5.2.
306Zadanie 5.3.
306Zadanie 5.4.
306Zadanie 5.5.
306Zadanie 5.8.
307Zadanie 5.9.
307Zadanie 5.10.
307Zadanie 33.
313Zadanie 35.
313Zadanie 36.
314Zadanie 38.
314Zadanie 39.
314Zadanie 40.
314Zadanie 41.
314Zadanie 45.
315Zadanie 46.
315Zadanie 47.
315Zadanie 50.
315Zadanie 51.
315Zadanie 52.
315
