![]()
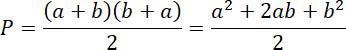
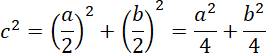
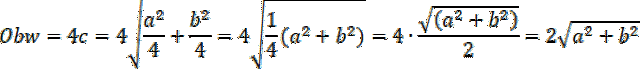
I, III — prawdziwe; II, IV — fałszywe

Dany jest romb o przekątnych długości a i b. Przekątną rombu o długości a zwiększono o b, a drugą przekątną tego rombu, o długości b, zwiększono o a. Teraz przekątne rombu mają równe długości i przecinają się w połowie.
I. Powstała figura jest kwadratem. Prawda.
II. Pole otrzymanej figury jest dwa razy większe od pola rombu przed zmianą długości przekątnych.
Pole przed zmianą:
![]() . Pole po zmianie:
. Pole po zmianie:
![]()
Fałsz.
III. Obwód rombu przed zmianą długości przekątnych wynosił
![]() . Oblicz długość boku rombu z twierdzenia Pitagorasa, za przyprostokątne Musisz podstawić połowę długości przekątnej:
. Oblicz długość boku rombu z twierdzenia Pitagorasa, za przyprostokątne Musisz podstawić połowę długości przekątnej:
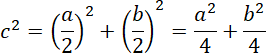
Obwód będzie równy 4c:
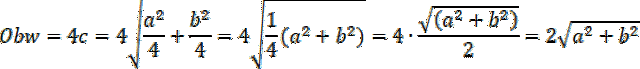
Prawda.
IV. Połowa pola rombu przed zmianą długości przekątnych była równa 0,5ab.
Fałsz. Pole przed zmianą:
![]() , czyli połowa pola to
, czyli połowa pola to
![]() .
.
