W tym zadaniu ustal, ile wynoszą współrzędne punktu C, który wraz z punktami A = (3, 4) i B = (3, 10) jest wierzchołkiem trójkąta równoramiennego ABC o polu równym 15. Przyjmij, że odcinek AB jest podstawą trójkąta.
10 – 4 = 6
![]()
![]()
![]()
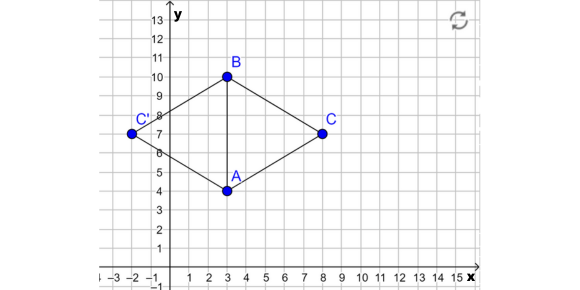
Punkt C może mieć współrzędne (8, 7) lub (-2, 7).

Najpierw ustal, ile wynosi długość podstawy. W tym celu oblicz odległość między punktami A i B. Zauważ, że współrzędne x-owe są takie same, czyli punkty A i B leżą na tej samej linii. Aby obliczyć odległość między punktami od większej współrzędnej y-owej odejmij mniejszą:
10 – 4 = 6
Znając długość podstawy i pole oblicz wysokość trójkąta:
![]()
![]()
![]()
Zwróć uwagę, że jest to trójkąt równoramienny, więc jego wysokość dzieli podstawę na dwa równe odcinki. Zatem, wierzchołek C leży w odległości 5 od podstawy. Narysuj w układzie współrzędnych podany trójkąt, zauważ, że wierzchołek C może leżeć na lewo i na prawo od odcinka AB.

Zadanie 6
65Zadanie 8
66Zadanie 10
66Zadanie 11
66Zadanie 14
66Zadanie 15
67Zadanie 16
67Zadanie 1
68Zadanie 2
68Zadanie 3
68Zadanie 6
68Zadanie 7
68Zadanie 8
69Zadanie 9
69Zadanie 10
69Zadanie 11
69Zadanie 13
70Zadanie 14
70Zadanie 16
71Zadanie 17
71Zadanie sprawdzające 3
72Zadanie 1
72Zadanie 2
72Zadanie 4
72Zadanie 5
72Zadanie 9
73Zadanie 10
73Zadanie 12
73Zadanie 13
74Zadanie 14
74Zadanie 1
75Zadanie 2
75Zadanie 3
75Zadanie 7
76Zadanie 8
76Zadanie 9.
76Zadanie 14
77Zadanie 19
77Zadanie 1
78Zadanie 3
79Zadanie 5
79Zadanie 6
79Zadanie 7
80Zadanie 8
80Zadanie 10
80Zadanie 11
80Zadanie 12
80Zadanie 17
81Zadanie 2
82Zadanie 6
83Zadanie 7
83Zadanie 8
83Zadanie 9
83Zadanie 10
83Zadanie 11
83Zadanie 12
84Zadanie 14
84Zadanie 1
85Zadanie 2
85Zadanie 3
85Zadanie 6
86Zadanie 7
86Zadanie 8
86Zadanie 9
87Zadanie 10
87Zadanie 11
87Zadanie 12
87Zadanie 14
87Zadanie 15
88Zadanie 17
88Zadanie 1
89Zadanie 4
89Zadanie 5
90Zadanie 7
90Zadanie 8
90Zadanie 9
90Zadanie 10
91Zadanie 11
91Zadanie 15
91Zadanie 1
93Zadanie 2
93Zadanie 3
93Zadanie 4
94Zadanie 5
94Zadanie 6
94Zadanie 7
94Zadanie 8
94Zadanie 10
95Zadanie 11
95
