Zadanie
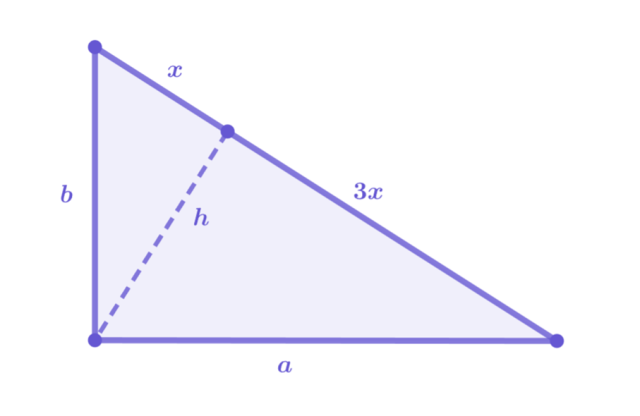
Dany jest trójkąt prostokątny, w którym wysokość wychodzi z kąta 90°. Dzieli ona przeciwprostokątną na 2 odcinki w taki sposób, że jeden z nich jest 3 razy dłuższy od drugiego.
W wyniku obrotu tego trójkąta wokół kolejno jednej i drugiej przyprostokątnej powstają dwa stożki. Udowodnij, że ich objętości pozostają w stosunku
.
Rozwiązanie
Wysokość h rozpisz ze wzoru na wysokość poprowadzoną z kąta prostego:
Zapisz układ dotyczący trójkątów powstałych przez poprowadzenie wysokości h:
Od równania pierwszego odejmij drugie:
Z twierdzenia Pitagorasa dotyczącego całego trójkąta:
Wstaw wartość a2 wyprowadzoną wyżej:
Stąd:
Rozpatrz poszczególne stożki:
1)
– promień podstawy
– wysokość
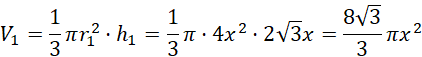
2)
– promień podstawy
– wysokość
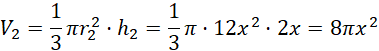
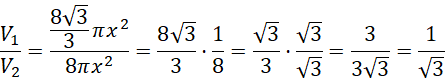
Co należało wykazać.
Wyjaśnienie
Stwórz rysunek pomocnicy. Zapisz długość przeciwprostokątnej jako sumę dwóch odcinków pozostających w podanym stosunku, np.: x i 3x.
Korzystając ze wzoru na wysokość poprowadzoną z kąta prostego oraz twierdzenia Pitagorasa dotyczącego poszczególnych trójkątów, zapisz uzależnij długości przyprostokątnych od x.
Rozpatrz stożki powstałe poprzez obrót trójkąta wokół poszczególnych przyprostokątnych.
Oblicz ich objętości i zapisz ich stosunek. Zauważ, że jest on równy temu podanemu w tezie, co kończy dowód.
Matematyka - wybrane pytania
REKLAMA
Zadania z tego działu
6. Geometria przestrzenna. Bryły obrotowe
144
Walec
144
Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146
Stożek
147
Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149
Kula i sfera
150
Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150
Bryły obrotowe – zadania różne
151
Zadanie 6.74.
152
Podobieństwo figur w przestrzeni
153
Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153
Zastosowanie analizy matematycznej w rozwiązywaniu zadań z geometrii przestrzennej
155
Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157
Test sprawdzający do rozdziału 6.
157
Zadania powtórzeniowe do rozdziału 6.
158
Zadanie 16.
159