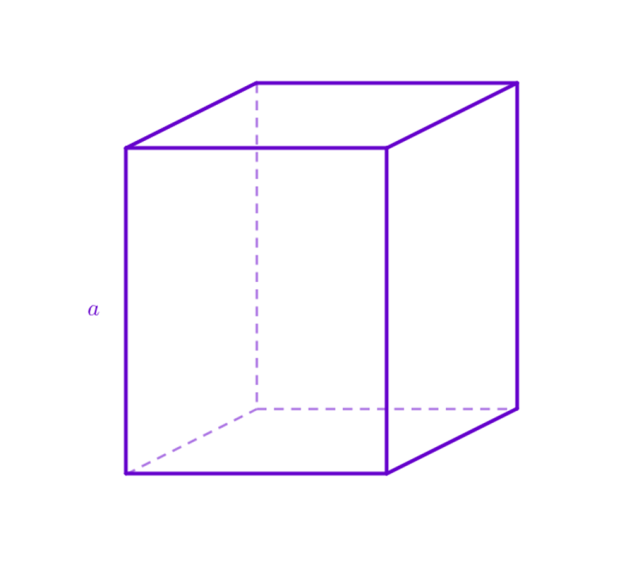
Oznacz długość krawędzi bocznej jako 𝑎. Przedział, do którego należy zmienna to:
![]()
Wyznacz długość krawędzi podstawy. Suma długości krawędzi podstawy jest równa:
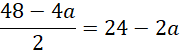
Długość pojedynczej krawędzi wynosi:
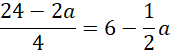
Objętość graniastosłupa wyraża się wzorem:
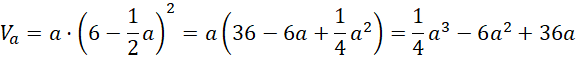
Wyznacz miejsce zerowe pochodnej tej funkcji:
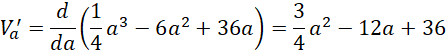
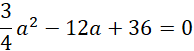
![]()
![]()
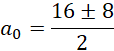
![]()
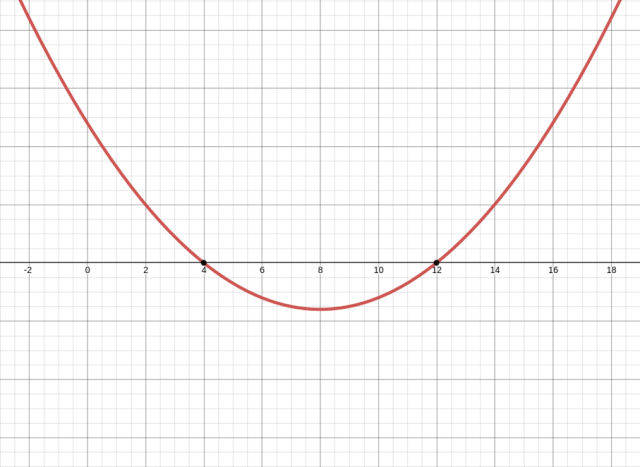
Pochodna zmienia znak z dodatniej na ujemną w punkcie 𝑎 = 4, czyli jest maksimum lokalnym.
Długość krawędzi podstawy jest równa:
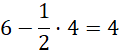
Zatem ten graniastosłup ma wymiary
![]() – sześcian.
– sześcian.
Objętość jest równa:
![]()
Odp. Graniastosłup o maksymalnej objętości to sześcian o krawędzi 4 cm i objętości 64 cm3.

Oznacz krawędź boczną jako zmienną i wyznacz przedział wartości (krawędź musi mieć długość i suma krawędzi bocznych nie może przekraczać sumy wszystkich krawędzi graniastosłupa). Oblicz długość krawędzi bocznej i oblicz objętość bryły. Miejsca zerowe pochodnej wyznaczonej funkcji wskazują na prawdopodobne ekstrema lokalne. Sprawdź, czy pochodna zmienia znak dla wyznaczonej wartości – masz wtedy do czynienia z ekstremum lokalnym.