Dany jest pewien stożek o długości tworzącej równej 𝑑. Udowodnij, że odcinek będący częścią wspólną stożka oraz prostej zawierającej środek wysokości stożka oraz równoległej do jednej z tworzących, ma długość
.
Z:
T:
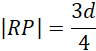
D:
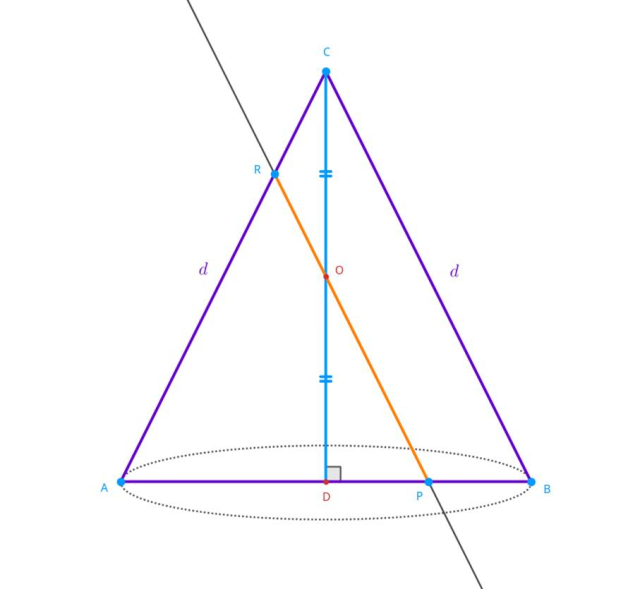
Zauważ, że skoro odcinki RP i CB są równoległe, oraz kąty ARP, ACB i APR, ABC są kątami odpowiadającymi, to mamy:
Wynika z tego, że masz podobieństwo między trójkątami:
Oblicz skalę podobieństwa trójkąta ODP do CDB wiedząc, że wysokość przekroju została podzielona na dwie równe części:
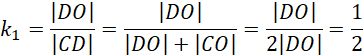
Czyli:
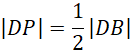
Spodek wysokości przekroju stożka D dzieli odcinek AB na dwa odcinki o równych długościach: AD i DB (trójkąty ACD i BCD są przystające). Zatem:
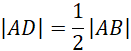
Oblicz skalę podobieństwa trójkąta APR do ABC:
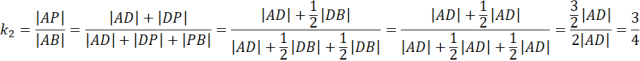
Oblicz długość odcinka RP:
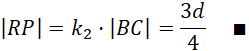
Użyj własności kątów odpowiadających przy prostych równoległych, by znaleźć podobieństwo wśród trójkątów znajdujących się w przekroju osiowym. Oblicz skalę podobieństwa między figurami podobnymi, by otrzymać skalę podobieństwa trójkąta APR do trójkąta ABC (przekroju osiowego).