Dany jest pewien stożek, którego przekrój osiowy jest trójkątem równobocznym o polu
![]() cm2. W bryłę wpisano walec w taki sposób, że jedna jego podstawa zawiera się w podstawie stożka, a druga podstawa jest styczna całym okręgiem do powierzchni bocznej stożka. Wyznacz maksimum objętości tego walca.
cm2. W bryłę wpisano walec w taki sposób, że jedna jego podstawa zawiera się w podstawie stożka, a druga podstawa jest styczna całym okręgiem do powierzchni bocznej stożka. Wyznacz maksimum objętości tego walca.
Wykorzystaj wzór wyznaczony w podpunkcie a):
![]()
Wyznacz miejsce zerowe pochodnej tej funkcji:
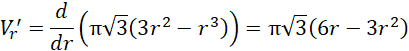
![]()
![]()
![]()
![]()
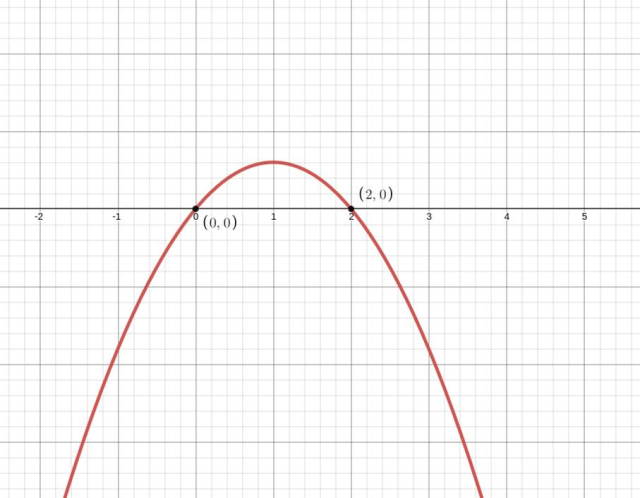
Pochodna zmienia znak z dodatniego na ujemny w wyznaczonym punkcie – masz do czynienia z maksimum lokalnym.
Podstaw otrzymaną wartość do wzoru na objętość walca:
![]()
Odp. Maksymalna objętość tak wpisanego walca wynosi
![]() cm3.
cm3.

Miejsca zerowe pochodnej wyznaczonej funkcji wskazują na prawdopodobne ekstrema lokalne. Sprawdź, czy pochodna zmienia znak dla wyznaczonej wartości – masz wtedy do czynienia z ekstremum lokalnym. Oblicz objętość walca dla otrzymanej wartości, korzystając z wyprowadzonych wzorów.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
