Dany jest pewien równoległobok, którego miara kąta ostrego wynosi 30°, a długości jego boków wiadomo, że ich różnica wynosi 7 cm. Z figury utworzono bryłę obrotową poprzez obrót wokół dłuższego boku. Wiedząc, że pole powierzchni całkowitej tak utworzonej bryły wynosi 184π cm2, oblicz jej objętość.
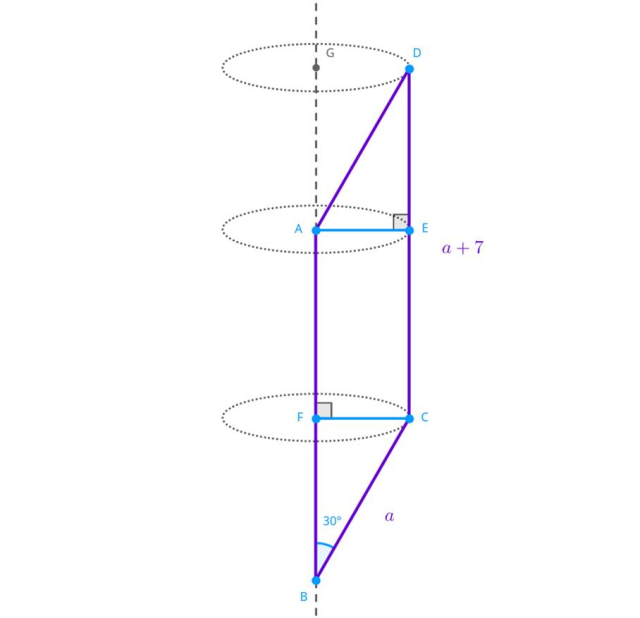
Oblicz długość promienia obrotu FC:
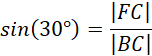
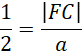
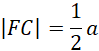
Na pole powierzchni całkowitej bryły składają się dwie powierzchnie boczne stożków o tworzących BC i AD oraz pole powierzchni bocznej walca o wysokości CD. Zatem:
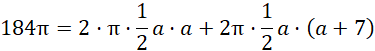
![]()
![]()
![]()
![]()
![]()
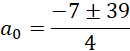
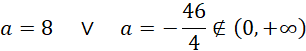
Zauważ, że objętość bryły powstałej z obrotu równoległoboku to to samo, co objętość walca FCDG. Oblicz jego objętość:
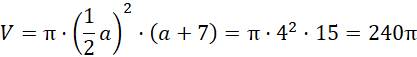
Odp. Objętość bryły wynosi 240π cm2.

Skorzystaj z definicji funkcji trygonometrycznych w trójkącie prostokątnym, żeby obliczyć wysokość równoległoboku. Podziel powierzchnię bryły na znajome Ci powierzchnie, dla których znane są Ci wzory na ich pola. Oblicz długość boku równoległoboku, uzależniając go od podanego w treści zadania pola powierzchni bryły. Oblicz objętość bryły (zauważ, że po odcięciu stożka utworzonego przez trójkąt FBC i umieszczeniu go na miejscu trójkąta GAD otrzymuje się walec o tej samej objętości, co bryła z zadania, co uzasadnia użycie wzoru na objętość walca).

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
