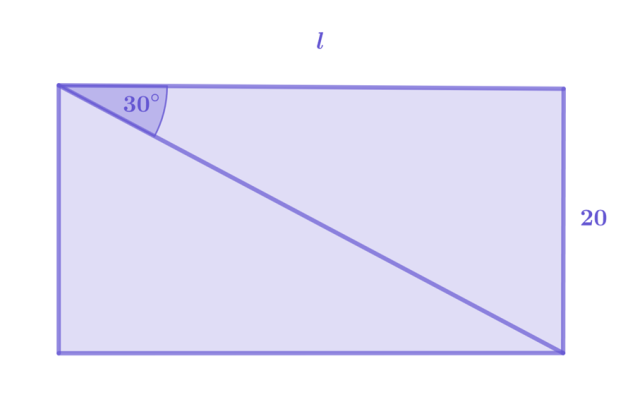
Dany jest walec o wysokości 20. Jego powierzchnia boczna to prostokąt, którego jednym bokiem jest wspomniana wysokość. Kąt pomiędzy drugim z jego boków a przekątną ma miarę 30°. Wyznacz pole całkowitej powierzchni walca.
Oznaczenia:
r – promień podstawy walca
h = 20 – wysokość walca
l – drugi z boków rozpatrywanego prostokąta
Powierzchnia boczna walca:
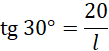
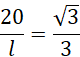
![]()
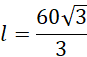
![]()
Długość boku l jest jednocześnie obwodem podstawy walca, zatem:
![]()
![]()
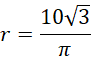
Pole podstawy walca:
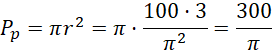
Pole powierzchni bocznej:
![]()
Pole powierzchni całkowitej jest sumą:
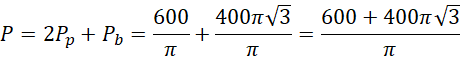

Naszkicuj powierzchnię boczną walca i wyznacz jej drugi bok z funkcji trygonometrycznych.
Zauważ, że bok ten jest jednocześnie obwodem koła w podstawie. Oblicz promień tej podstawy.
Mając wszystkie dane wyznacz pole powierzchni całkowitej jako sumę pola powierzchni bocznej oraz pól obu podstaw.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
