Dany jest prostokąt, w którym jeden bok jest dwukrotnie dłuższy od drugiego. Podaj iloraz pól całkowitej powierzchni dwóch walców, które powstają w wyniku obrotu danego prostokąta wokół jego obu różnych osi symetrii.
Oznacz boki prostokąta jako:
![]()
Walec pierwszy:
Promień:
![]()
Wysokość:
![]()
Pole podstawy:
![]()
Pole powierzchni bocznej:
![]()
Pole powierzchni całkowitej:
![]()
Walec drugi:
Promień:
![]()
Wysokość:
![]()
Pole podstawy:
![]()
Pole powierzchni bocznej:
![]()
Pole powierzchni całkowitej:
![]()
Szukany stosunek:
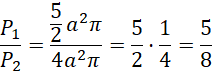

Wprowadź oznaczenia poszczególnych wielkości.
Wyznacz na nich pola powierzchni całkowitej obu rozpatrywanych walców.
Oblicz szukany stosunek dzieląc otrzymane wyniki.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
