Dany jest pewien stożek, o którym wiadomo, że kąt między jego tworzącą a płaszczyzną podstawy ma miarę α. Przez bryłę przeprowadzono płaszczyznę zawierającą wierzchołek stożka, nachyloną do płaszczyzny podstawy pod kątem ostrym o mierze β. Powstały w ten sposób przekrój – trójkąt równoramienny – ma miarę kąta między ramionami równą γ. Udowodnij, że zachodzi równość
.
Z:
𝑙 – długość tworzącej stożka,
ℎ - wysokość przekroju opuszczona na podstawę należącą do powierzchni podstawy stożka,
𝐻 – wysokość stożka,
α – kąt nachylenia tworzącej stożka do płaszczyzny podstawy,
β – kąt nachylenia płaszczyzny przekroju do płaszczyzny podstawy,
γ – kąt rozpostarty między ramionami przekroju.
T:
D:
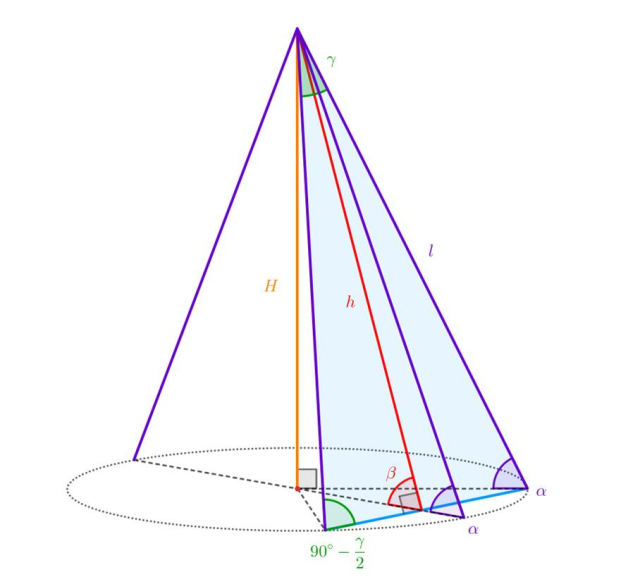
Skorzystaj z definicji funkcji trygonometrycznych:
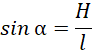
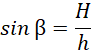
Zatem:
Skorzystaj z własności kątów wewnętrznych trójkąta równoramiennego, by wyznaczyć miarę kąta przy podstawie przekroju:
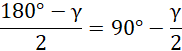
Zauważ, że ramię przekroju ma długość równą tworzącej stożka. Skorzystaj z definicji funkcji trygonometrycznych:
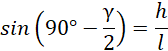
Z wzorów redukcyjnych:
Wykorzystaj pierwszą wyprowadzoną równość:
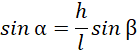
Podstaw do wzoru:
Opisz odpowiednio kluczowe długości odcinków w stożku, a następnie wyraź ich ilorazy jako sinusy kątów podanych w treści zadania. Uprość wyrażenie za pomocą wzorów redukcyjnych i podstaw do wyprowadzonej relacji.