Dana jest kula o promieniu długości 3. W kulę wpisano ostrosłup prawidłowy czworokątny tak, że wierzchołki podstawy należą do powierzchni kuli, a wierzchołek ostrosłupa i środek kuli pokrywają się. Oblicz maksymalną objętość wpisanego ostrosłupa.
Wykorzystaj wzór wyznaczony w podpunkcie a):
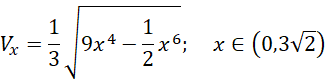
Wyznacz miejsce zerowe pochodnej tej funkcji. Zauważ, że pierwiastek jest funkcją monotonicznie rosnącą oraz ciągłą na przedziale danym przez funkcję (objętość ostrosłupa jest zawsze dodatnia). Zatem:
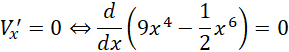
![]()
![]()
![]()
![]()
![]()
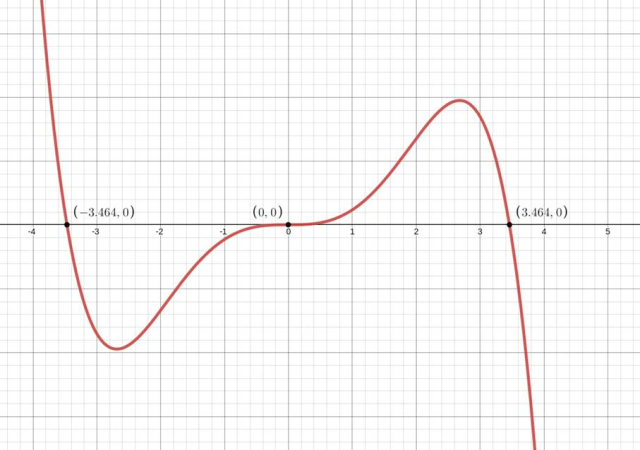
Pochodna zmienia znak z dodatniego na ujemny w wyznaczonym punkcie – masz do czynienia z maksimum lokalnym.
Oblicz objętość ostrosłupa:
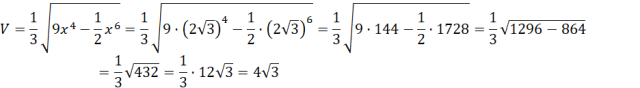
Odp. Maksymalna objętość ostrosłupa skonstruowanego w taki sposób wynosi
![]() .
.

Miejsca zerowe pochodnej wyznaczonej funkcji wskazują na prawdopodobne ekstrema lokalne. Sprawdź, czy pochodna zmienia znak dla wyznaczonej wartości – masz wtedy do czynienia z ekstremum lokalnym. Oblicz objętość ostrosłupa dla otrzymanej wartości, korzystając z wyprowadzonego wzoru na objętość bryły.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
