Dana jest kula o promieniu długości 3. W kulę wpisano ostrosłup prawidłowy czworokątny tak, że wierzchołki podstawy należą do powierzchni kuli, a wierzchołek ostrosłupa i środek kuli pokrywają się. Wiedząc, że długość krawędzi podstawy ostrosłupa wynosi 𝑥, wyznacz wzór opisujący objętość ostrosłupa względem tej długości.
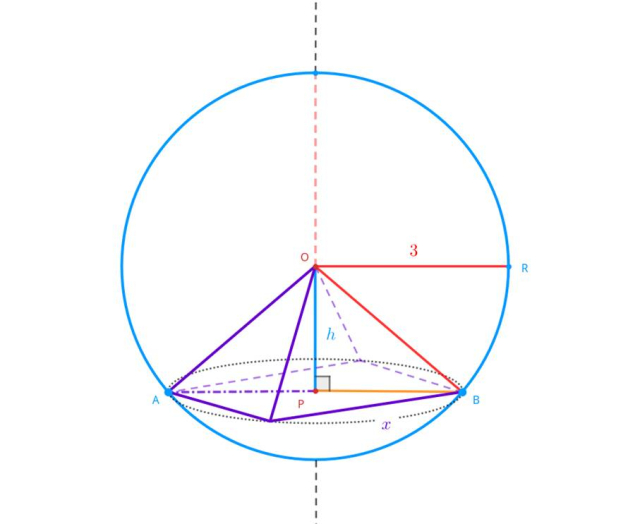
Oznacz krawędzi podstawy ostrosłupa jako 𝑥, a wysokość bryły jako ℎ. Zauważ, że odcinek PB to połowa długości przekątnej podstawy – kwadratu – czyli jego długość to:
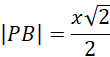
Uzależnij wysokość ostrosłupa od długości krawędzi podstawy:
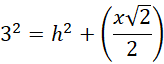
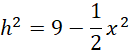
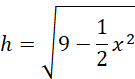
Wyznacz dziedzinę długości krawędzi podstawy ostrosłupa:
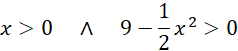
![]()
![]()
![]()
Wyznacz objętość ostrosłupa względem długości krawędzi podstawy:
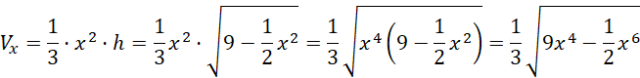

Oznacz krawędź podstawy ostrosłupa oraz jego wysokość jako zmienne. Oblicz długość połowy przekątnej podstawy, a następnie wysokość ostrosłupa względem długości krawędzi podstawy. Podstaw otrzymane długości do wzoru na objętość ostrosłupa i wyznacz dziedzinę.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
