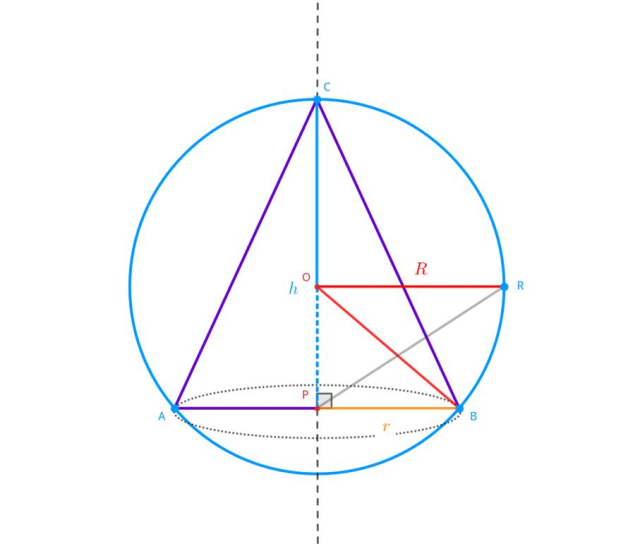
Uzależnij promień podstawy stożka od pozostałych długości stożka:
![]()
![]()
![]()
![]()
Wyznacz dziedzinę wysokości stożka:
![]()
![]()
![]()
![]()
Wyznacz objętość wpisanego stożka względem jego wysokości:
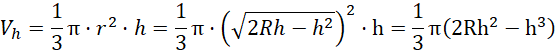
Wyznacz miejsce zerowe pochodnej tej funkcji:
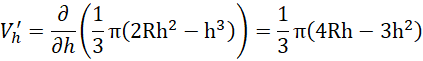
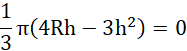
![]()
![]()
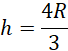
Pochodna to funkcja kwadratowa o ujemnym znaku współczynnika przy największej potędze. Otrzymane miejsce zerowe jest „po prawej stronie”, więc znak zmienia się z dodatniego na ujemny. Otrzymana wartość jest maksimum lokalnym funkcji objętości.
Oblicz długość promienia podstawy wpisanego stożka:
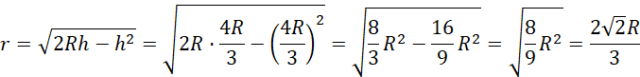
Odp. Stożek wpisany w kulę o maksymalnej objętości ma promień podstawy długości
![]() i wysokość
i wysokość
![]() .
.

Oznacz promień podstawy oraz wysokość stożka wpisanego jako zmienne. Oblicz długość promienia podstawy względem wysokości bryły i wyznacz przedział wartości. Podstaw otrzymane długości do wzoru na objętość stożka. Oblicz pochodną cząstkową funkcji objętości stożka względem długości wysokości. Miejsca zerowe pochodnej wyznaczonej funkcji wskazują na prawdopodobne ekstrema lokalne. Sprawdź, czy pochodna zmienia znak dla wyznaczonej wartości – masz wtedy do czynienia z ekstremum lokalnym. Oblicz długość promienia podstawy dla otrzymanej wysokości, korzystając z wyprowadzonych wzorów.