Dany jest pewien prostopadłościan. Wiadomo o nim, że stosunek długości krawędzi w podstawie wynosi 2 : 1 oraz że objętość bryły to 72 litry. Wyznacz długości krawędzi prostopadłościanu, dla których pole powierzchni jest minimalne.
Wzór na pole powierzchni bryły jest równe:
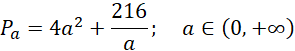
Wyznacz miejsce zerowe pochodnej tej funkcji:
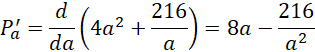
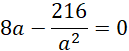
![]()
![]()
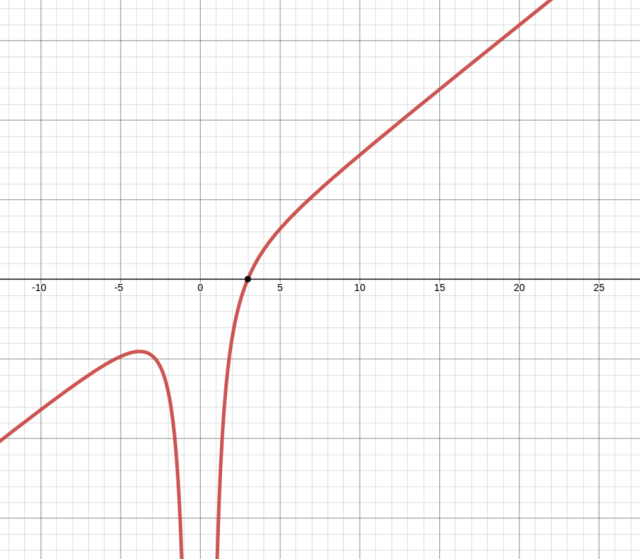
Pochodna zmienia znak z ujemnego na dodatni w wyznaczonym punkcie – masz do czynienia z minimum lokalnym.
Krawędzie podstawy prostopadłościanu mają długości: 3 i 6 dm. Wysokość prostopadłościanu to:
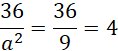
Odp. Prostopadłościan o minimalnym polu powierzchni całkowitej ma wymiary
![]() cm.
cm.

Miejsca zerowe pochodnej wyznaczonej funkcji wskazują na prawdopodobne ekstrema lokalne. Sprawdź, czy pochodna zmienia znak dla wyznaczonej wartości – masz wtedy do czynienia z ekstremum lokalnym.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
