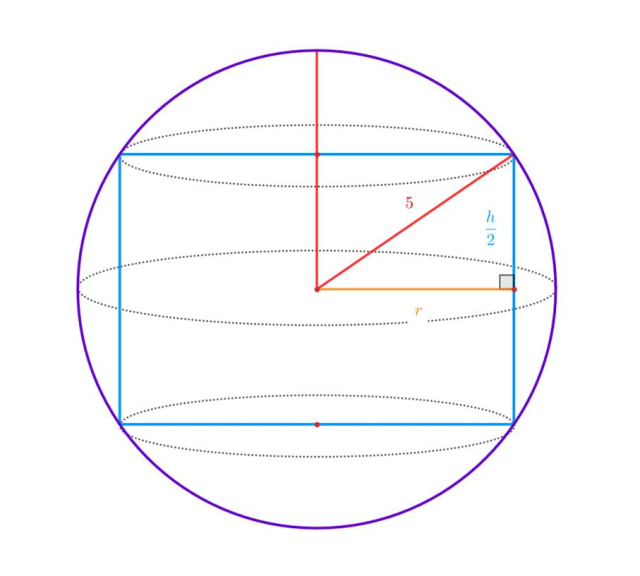
Oznacz promień podstawy walca jako 𝑟 i wysokość walca jako ℎ. Uzależnij wysokość walca od długości promienia podstawy wpisanego walca:
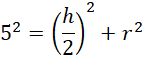
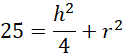
![]()
![]()
Długość promienia podstawy walca nie może przekroczyć długości promienia kuli, zatem:
![]()
Wyznacz wzór na pole powierzchni bocznej walca względem promienia podstawy walca:
![]()
Wyznacz miejsce zerowe pochodnej tej funkcji. Zauważ, że pierwiastek jest funkcją monotonicznie rosnącą oraz ciągłą na przedziale danym przez funkcję (pole powierzchni bocznej walca jest zawsze dodatnie). Zatem:
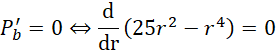
![]()
![]()
![]()
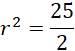
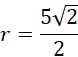
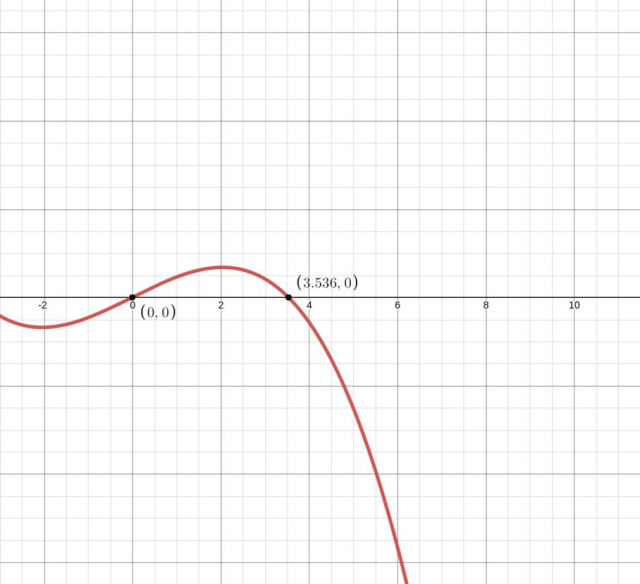
Pochodna zmienia znak z dodatniego na ujemny w wyznaczonym punkcie – masz do czynienia z maksimum lokalnym.
Oblicz wysokość walca:
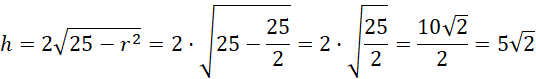
Oblicz objętość bryły:
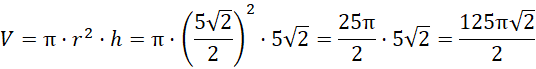
Odp. Objętość wpisanego walca o maksymalnym polu powierzchni bocznej wynosi
![]() cm3.
cm3.

Oznacz promień podstawy oraz wysokość walca jako zmienne. Oblicz wysokości bryły względem promienia podstawy i wyznacz przedział wartości. Podstaw otrzymane długości do wzoru na pole powierzchni bocznej walca. Miejsca zerowe pochodnej wyznaczonej funkcji wskazują na prawdopodobne ekstrema lokalne. Sprawdź, czy pochodna zmienia znak dla wyznaczonej wartości – masz wtedy do czynienia z ekstremum lokalnym. Oblicz wysokość bryły oraz jej objętość dla otrzymanych wartości, korzystając z wyprowadzonych wzorów.