Założenia:
Pole rozpatrywanego trójkąta:
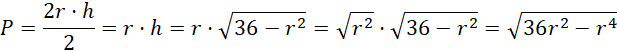
Szukane jest największe pole. Powyższe wyrażenie osiągnie największą wartość, gdy wyrażenie pod pierwiastkiem osiągnie największą wartość, co wynika z monotoniczności funkcji
.
Rozpatrz poniższą funkcję zmiennej r i znajdź jej największą wartość:
Oblicz jej pochodną:
gdy:
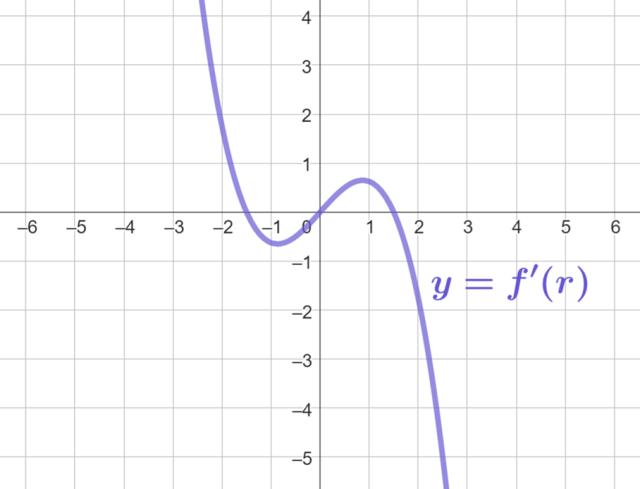
Naszkicuj wykres pochodnej:
|
|
|
|
|
|
| |
| f’ | + | 0 | - | 0 | + | 0 | - |
| f | rosnąca | maks. lok. | malejąca | min. lok. | rosnąca | maks. lok. | malejąca |
W punktach r = 0, r = 3
funkcja f osiąga maksimum lokalne.
Zatem w punkcie r = 3
funkcja f osiąga największą wartość.
Przejdź do obliczania objętości stożka o promieniu podstawy r = 3
:
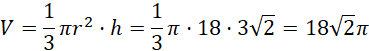
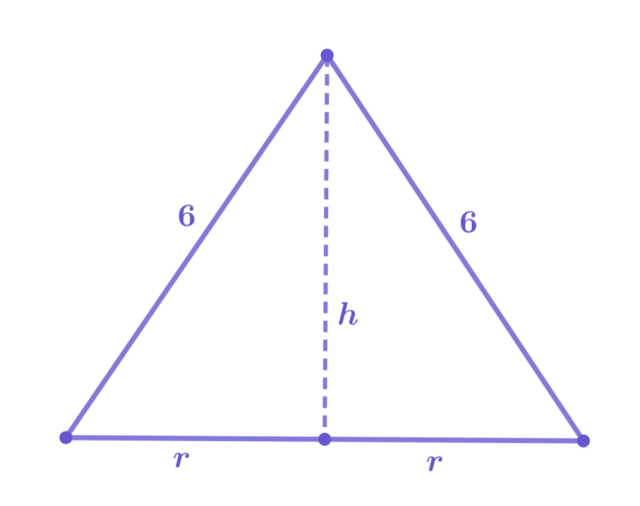
Stwórz rysunek pomocnicy. Uzależnij wysokość trójkąta będącego przekrojem od promienia podstawy stożka. Pamiętaj o odpowiednich założeniach wynikających z faktu, że poszczególne wielkości geometryczne muszą być dodatnie.
Zdefiniuj funkcję pola rozpatrywanego trójkąta od długości promienia. Znajdź największą wartość tej funkcji. W tym celu oblicz jej pochodną, naszkicuj wykres i na jego podstawie zbadaj przebieg funkcji pierwotnej.
Oblicz wartości funkcji dla argumentów, dla których funkcja ta osiąga ekstrema lokalne. Odczytaj wartość tego promienia, dla którego rozpatrywana funkcja osiąga największą wartość.
Mając szukany promień, oblicz wysokość stożka i jego objętość.