Na równoleżniku 60° N znajduje się pewne miasto. W wyniku ruchu obrotowego Ziemi, pokonuje ono w ciągu 1h pewien dystans. Wyznacz go zakładając, że pełen obrót Ziemi trwa 24h.
R = 6300 km – promień kuli ziemskiej
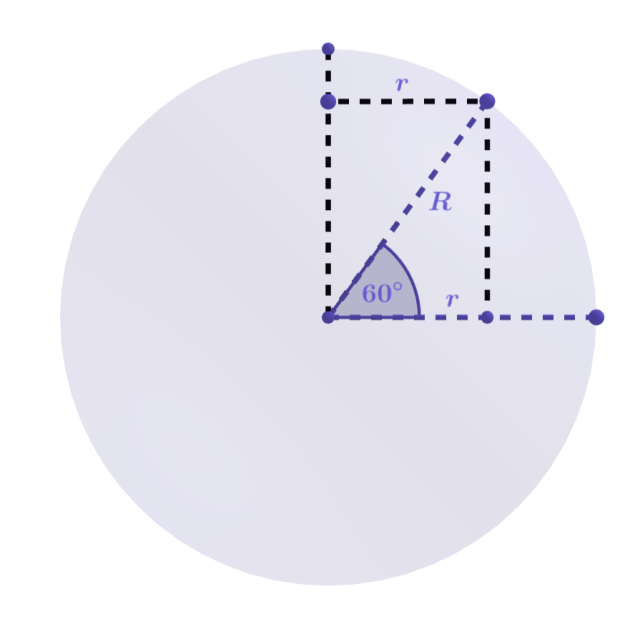
r – promień koła będącego przekrojem odpowiadającym rozpatrywanemu równoleżnikowi
![]()
![]()

![]()
![]()
Obwód koła o promieniu r jest szukanym równoleżnikiem. Wynosi on:
![]()
Jest to droga zakreślona przez to miasto w ciągu 24h.
Zatem szukanym wynikiem będzie liczba:
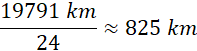
Odpowiedź: około 825 km

Stwórz rysunek pomocniczy.
Zauważ, że długość rozpatrywanego równoleżnika jest obwodem koła będącego przekrojem kuli ziemskiej odpowiadającego podanej szerokości geograficznej.
Korzystając z funkcji trygonometrycznej cosinus oblicz promień tego przekroju.
Oblicz długość równoleżnika korzystając ze wzoru l = 2πr. Na koniec wynik ten podziel przez 24.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
