Dany jest walec, którego powierzchnia boczna po rozwinięciu jest kwadratem. Wyznacz jej pole, jeśli objętość całego walca to
![]() cm3.
cm3.
Oznaczenia:
r – promień podstawy walca
h – wysokość walca
Powierzchnia boczna dowolnego walca jest prostokątem, którego jeden bok pokrywa się z wysokością walca, a drugi z obwodem podstawy.
Skoro w tym przypadku jest ona kwadratem, to zachodzi równość:
![]()
Objętość walca:
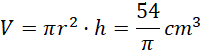
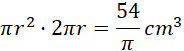
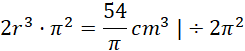
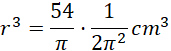
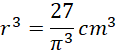
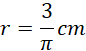
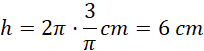
Pole boczne wynosi więc:
![]()

Zwróć uwagę na fakt, że powierzchnia boczna dowolnego walca jest prostokątem, którego jeden bok pokrywa się z wysokością, a drugi z obwodem podstawy walca. Z informacji z treści zadania wywnioskuj, że wymiary te są sobie równe.
Z podanej w zadaniu objętości wyznacz brakujące wymiary walca i wyznacz szukane pole powierzchni boczne.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
