Dana jest pewna kula. Pole jej koła wielkiego jest większe o 12,25π dm2 od pola przekroju tej samej kuli. Wyznacz odległość między tymi płaszczyznami wiedząc, że są one do siebie równoległe.
Oznaczenia:
R – promień całej kuli i jednocześnie jej koła wielkiego
r – promień rozpatrywanego przekroju
x – szukana odległość
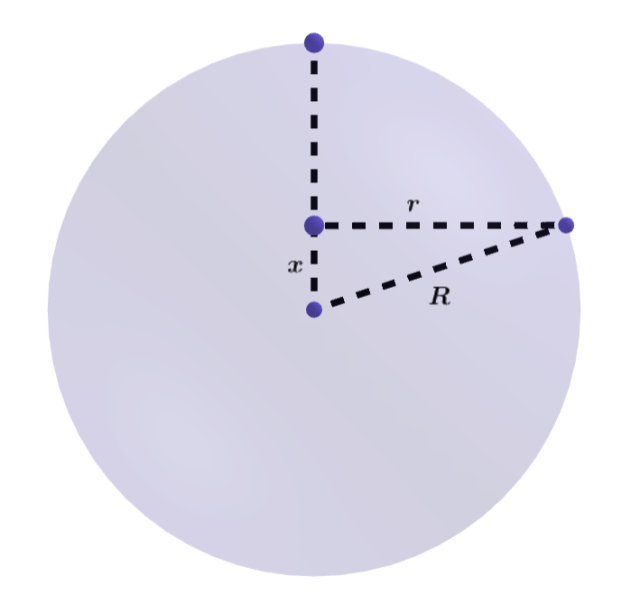
Z rysunku:
![]()
![]()
Z zależności między odpowiednimi polami z treści zadania:
![]()
![]()
![]()
Wstaw tę wartość do równości wyżej:
![]()
![]()

Wprowadź odpowiednie oznaczenia i stwórz rysunek pomocniczy.
Korzystając z twierdzenia Pitagorasa zapisz szukaną odległość jako odpowiednią różnicę kwadratów promieni.
Zapisz podaną w treści zależność między polami i wstaw ją do wcześniejszej równości.
Wyznacz z niej szukaną odległość między płaszczyznami.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
