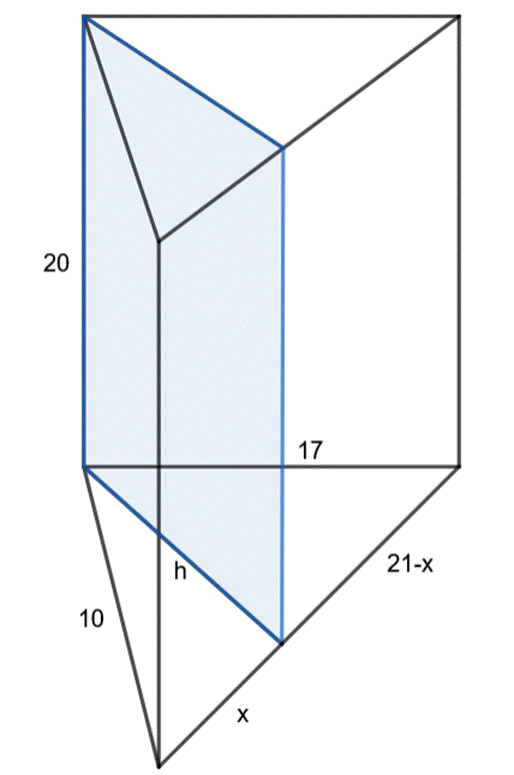
Wyznacz pole przekroju, jeśli krawędzie podstawy graniastosłupa prostego trójkątnego mają długość: 10 cm, 17 cm, 21 cm, wysokość jest równa 20 cm. Graniastosłup przecięto płaszczyzną, zawierającą najkrótszą wysokość podstawy i krawędź boczną, która ma punkt wspólny z tą wysokością.
![]()
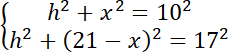
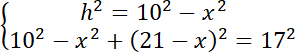
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Wykonaj rysunek pomocniczy. Zauważ, że skoro graniastosłup jest prosty, to wszystkie jego krawędzie boczne mają taką samą długość. Zauważ, że w podstawie powstały dwa trójkąty prostokątne. Skorzystaj z twierdzenia Pitagorasa, zapisz to za pomocą równań. Zauważ, że powstał układ dwóch równań z dwoma niewiadomymi. Wyznacz z nich wartości niewiadomych
![]() i
i
![]() . Na koniec oblicz pole przekroju – prostokąta.
. Na koniec oblicz pole przekroju – prostokąta.

Zadanie 5.1
78Zadanie 5.2
78Zadanie 5.4
78Zadanie 5.5
78Zadanie 5.6
79Zadanie 5.7
79Zadanie 5.8
79Zadanie 5.35
84Zadanie 5.37
84Zadanie 5.39
84Zadanie 5.40
84Zadanie 5.41
85Zadanie 5.42
85Zadanie 5.45
85Zadanie 5.46
85Zadanie 5.47
86Zadanie 5.50
86Zadanie 5.53
86Zadanie 5.55
87Zadanie 5.56
87Zadanie 5.57
87Zadanie 5.58
87Zadanie 5.60
87Zadanie 5.62
87Zadanie 5.63
88Zadanie 5.64
88Zadanie 5.65
88Zadanie 5.66
88Zadanie 5.67
88Zadanie 5.68
88Zadanie 5.69
88Zadanie 5.70
88Zadanie 5.71
89Zadanie 5.72
89Zadanie 5.73
89Zadanie 5.74
89Zadanie 5.75
89Zadanie 5.76
89Zadanie 5.77
90Zadanie 5.78
90Zadanie 5.79
90Zadanie 5.80
90Zadanie 5.81
91Zadanie 5.82
91Zadanie 5.83
91Zadanie 5.85
91Zadanie 5.86
92Zadanie 5.87
92Zadanie 5.88
92Zadanie 5.100
93Zadanie 5.102
94Zadanie 5.107
94Zadanie 5.112
95Zadanie 5.119
96Zadanie 5.120
96Zadanie 5.122
96Zadanie 5.127
97Zadanie 5.130
97Zadanie 5.140
99Zadanie 5.142
99Zadanie 18
102Zadanie 19
102Zadanie 20
102Zadanie 21
102Zadanie 24
103Zadanie 25
103
