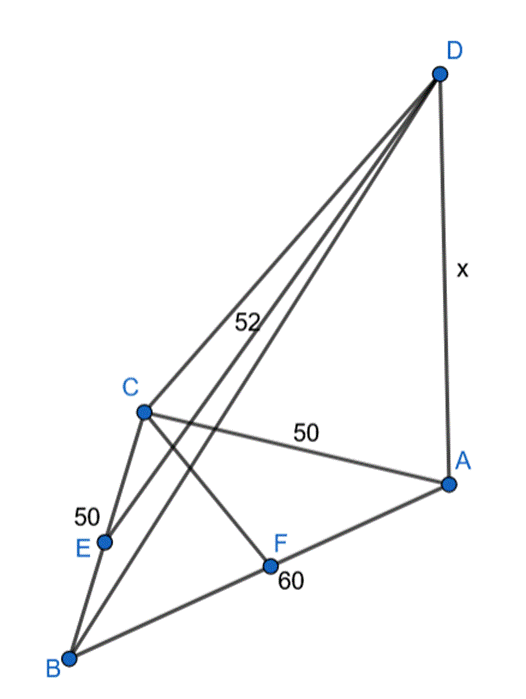
Wyznacz odległość punktu D od płaszczyzny (ABC), jeśli boki trójkąta ABC mają długość:
![]() , odcinek AD jest prostopadły do płaszczyzny (ABC), a odległość punktu D od prostej BC jest równa 52 cm.
, odcinek AD jest prostopadły do płaszczyzny (ABC), a odległość punktu D od prostej BC jest równa 52 cm.
![]()
![]()
![]()
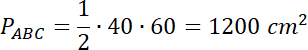
Rzutem prostopadłym odcinka DE jest odcinek AE, odcinki DE oraz BC są prostopadłe, więc korzystając z twierdzenia o trzech prostych prostopadłych: rzut odcinka AE jest prostopadły do odcinka BC, więc odcinek AE jest wysokością trójkąta ABC.
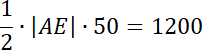
![]()
![]()
![]()
![]()
![]()

Wykonaj rysunek pomocniczy i skorzystaj z twierdzenia o trzech prostych prostopadłych: jeśli rzut prostopadły danej prostej
![]() jest prostopadły do pewnej prostej
jest prostopadły do pewnej prostej
![]() , to prosta
, to prosta
![]() jest również prostopadła do prostej
jest również prostopadła do prostej
![]() .
.
Następnie zauważ, że trójkąt ADE jest prostokątny. Skorzystaj z twierdzenia Pitagorasa, aby obliczyć długość odcinka
![]() .
.

Zadanie 5.1
78Zadanie 5.2
78Zadanie 5.4
78Zadanie 5.5
78Zadanie 5.6
79Zadanie 5.7
79Zadanie 5.8
79Zadanie 5.35
84Zadanie 5.37
84Zadanie 5.39
84Zadanie 5.40
84Zadanie 5.41
85Zadanie 5.42
85Zadanie 5.45
85Zadanie 5.46
85Zadanie 5.47
86Zadanie 5.50
86Zadanie 5.53
86Zadanie 5.55
87Zadanie 5.56
87Zadanie 5.57
87Zadanie 5.58
87Zadanie 5.60
87Zadanie 5.62
87Zadanie 5.63
88Zadanie 5.64
88Zadanie 5.65
88Zadanie 5.66
88Zadanie 5.67
88Zadanie 5.68
88Zadanie 5.69
88Zadanie 5.70
88Zadanie 5.71
89Zadanie 5.72
89Zadanie 5.73
89Zadanie 5.74
89Zadanie 5.75
89Zadanie 5.76
89Zadanie 5.77
90Zadanie 5.78
90Zadanie 5.79
90Zadanie 5.80
90Zadanie 5.81
91Zadanie 5.82
91Zadanie 5.83
91Zadanie 5.85
91Zadanie 5.86
92Zadanie 5.87
92Zadanie 5.88
92Zadanie 5.100
93Zadanie 5.102
94Zadanie 5.107
94Zadanie 5.112
95Zadanie 5.119
96Zadanie 5.120
96Zadanie 5.122
96Zadanie 5.127
97Zadanie 5.130
97Zadanie 5.140
99Zadanie 5.142
99Zadanie 18
102Zadanie 19
102Zadanie 20
102Zadanie 21
102Zadanie 24
103Zadanie 25
103
