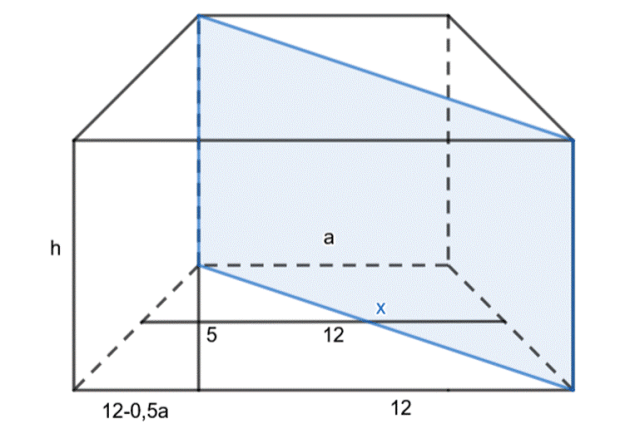
Wyznacz objętość graniastosłupa prostego, jeśli jego podstawą jest trapez równoramienny, którego wysokość jest równa 5 cm, a odcinek łączący środki ramion ma długość 12 cm. Przekrój graniastosłupa płaszczyzną, zawierającą krawędź boczną i przekątną podstawy, ma pole równe 130 cm2.
![]()
![]()
![]()
![]()
![]()
![]()
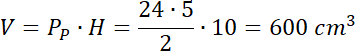

Wykonaj rysunek pomocniczy. Skorzystaj z tego, że odcinek łączący środki ramion trapezu jest dwa razy krótszy niż suma jego podstaw. Skorzystaj z twierdzenia Pitagorasa w trójkącie prostokątnym znajdującym się w podstawie, aby obliczyć długość jego przeciwprostokątnej.
Następnie ze wzoru na pole przekroju – prostokąta, wyznacz długość wysokości graniastosłupa i oblicz jego objętość.

Zadanie 5.1
78Zadanie 5.2
78Zadanie 5.4
78Zadanie 5.5
78Zadanie 5.6
79Zadanie 5.7
79Zadanie 5.8
79Zadanie 5.35
84Zadanie 5.37
84Zadanie 5.39
84Zadanie 5.40
84Zadanie 5.41
85Zadanie 5.42
85Zadanie 5.45
85Zadanie 5.46
85Zadanie 5.47
86Zadanie 5.50
86Zadanie 5.53
86Zadanie 5.55
87Zadanie 5.56
87Zadanie 5.57
87Zadanie 5.58
87Zadanie 5.60
87Zadanie 5.62
87Zadanie 5.63
88Zadanie 5.64
88Zadanie 5.65
88Zadanie 5.66
88Zadanie 5.67
88Zadanie 5.68
88Zadanie 5.69
88Zadanie 5.70
88Zadanie 5.71
89Zadanie 5.72
89Zadanie 5.73
89Zadanie 5.74
89Zadanie 5.75
89Zadanie 5.76
89Zadanie 5.77
90Zadanie 5.78
90Zadanie 5.79
90Zadanie 5.80
90Zadanie 5.81
91Zadanie 5.82
91Zadanie 5.83
91Zadanie 5.85
91Zadanie 5.86
92Zadanie 5.87
92Zadanie 5.88
92Zadanie 5.100
93Zadanie 5.102
94Zadanie 5.107
94Zadanie 5.112
95Zadanie 5.119
96Zadanie 5.120
96Zadanie 5.122
96Zadanie 5.127
97Zadanie 5.130
97Zadanie 5.140
99Zadanie 5.142
99Zadanie 18
102Zadanie 19
102Zadanie 20
102Zadanie 21
102Zadanie 24
103Zadanie 25
103
