Udowodnij, że trójkąty BCE i ADE są prostokątne, jeśli w równoległoboku ABCD przekątna DB jest jednocześnie wysokością poprowadzoną na boki AD i BC, proste DB i AC przecinają się w punkcie O, a odcinek EO jest prostopadły do płaszczyzny (ABCD).
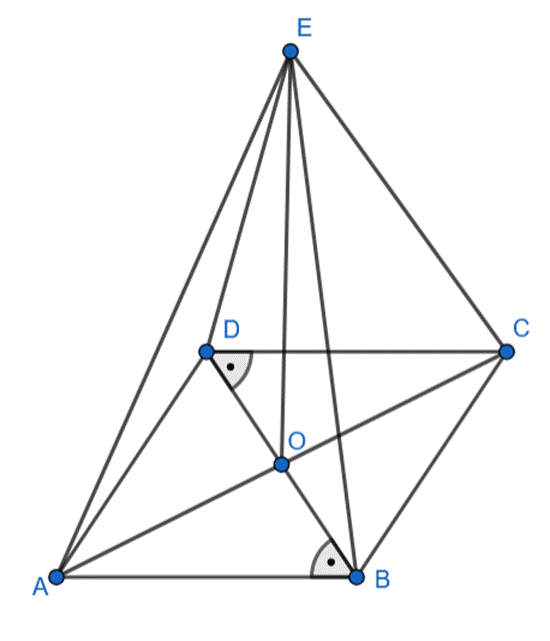
Rzutem odcinka BE jest odcinek BO, a rzutem odcinek DE jest odcinek DO. Z treści zadania wiadomo, że odcinki BO i BC oraz DO i AD są prostopadłe. Korzystając z twierdzenia o trzech prostych prostopadłych: aby odcinek BC był prostopadły do odcinka BE, to musi być prostopadły do odcinka BO – jest tak, analogicznie: aby odcinek AD był prostopadły do odcinka DE, to musi być prostopadły do odcinka DO. Więc trójkąty BCE i ADE są prostokątne.
To kończy dowód.

Skorzystaj z twierdzenia o trzech prostych prostopadłych: jeśli rzut prostopadły danej prostej
![]() jest prostopadły do pewnej prostej
jest prostopadły do pewnej prostej
![]() , to prosta
, to prosta
![]() jest również prostopadła do prostej
jest również prostopadła do prostej
![]() .
.

Zadanie 5.1
78Zadanie 5.2
78Zadanie 5.4
78Zadanie 5.5
78Zadanie 5.6
79Zadanie 5.7
79Zadanie 5.8
79Zadanie 5.35
84Zadanie 5.37
84Zadanie 5.39
84Zadanie 5.40
84Zadanie 5.41
85Zadanie 5.42
85Zadanie 5.45
85Zadanie 5.46
85Zadanie 5.47
86Zadanie 5.50
86Zadanie 5.53
86Zadanie 5.55
87Zadanie 5.56
87Zadanie 5.57
87Zadanie 5.58
87Zadanie 5.60
87Zadanie 5.62
87Zadanie 5.63
88Zadanie 5.64
88Zadanie 5.65
88Zadanie 5.66
88Zadanie 5.67
88Zadanie 5.68
88Zadanie 5.69
88Zadanie 5.70
88Zadanie 5.71
89Zadanie 5.72
89Zadanie 5.73
89Zadanie 5.74
89Zadanie 5.75
89Zadanie 5.76
89Zadanie 5.77
90Zadanie 5.78
90Zadanie 5.79
90Zadanie 5.80
90Zadanie 5.81
91Zadanie 5.82
91Zadanie 5.83
91Zadanie 5.85
91Zadanie 5.86
92Zadanie 5.87
92Zadanie 5.88
92Zadanie 5.100
93Zadanie 5.102
94Zadanie 5.107
94Zadanie 5.112
95Zadanie 5.119
96Zadanie 5.120
96Zadanie 5.122
96Zadanie 5.127
97Zadanie 5.130
97Zadanie 5.140
99Zadanie 5.142
99Zadanie 18
102Zadanie 19
102Zadanie 20
102Zadanie 21
102Zadanie 24
103Zadanie 25
103
