Udowodnij, że jeśli
![]() oraz
oraz
![]() , to prosta PQ jest równoległa do płaszczyzny
, to prosta PQ jest równoległa do płaszczyzny
![]() jeśli dane są punkty A, B należące do płaszczyzny
jeśli dane są punkty A, B należące do płaszczyzny
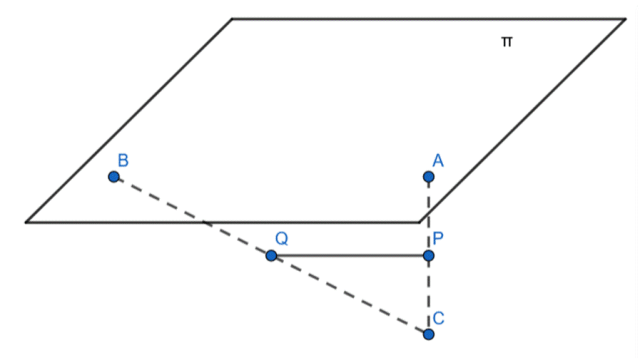
![]() oraz punkt C poza tą płaszczyzną. Punkt P należy do odcinka AC, a punkt Q – do odcinka BC.
oraz punkt C poza tą płaszczyzną. Punkt P należy do odcinka AC, a punkt Q – do odcinka BC.
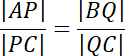
![]()

Wykonaj rysunek prezentujący treść zadania. Skorzystaj z twierdzenia odwrotnego do twierdzenia Talesa i zapisz proporcję, a następnie zauważ, że zachodzi twierdzenie odwrotnie do twierdzenia Talesa: Jeżeli odcinki wyznaczone przez dwie proste na jednym ramieniu kąta są proporcjonalne do odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu kąta, to proste te są równoległe.

Zadanie 5.1
78Zadanie 5.2
78Zadanie 5.4
78Zadanie 5.5
78Zadanie 5.6
79Zadanie 5.7
79Zadanie 5.8
79Zadanie 5.35
84Zadanie 5.37
84Zadanie 5.39
84Zadanie 5.40
84Zadanie 5.41
85Zadanie 5.42
85Zadanie 5.45
85Zadanie 5.46
85Zadanie 5.47
86Zadanie 5.50
86Zadanie 5.53
86Zadanie 5.55
87Zadanie 5.56
87Zadanie 5.57
87Zadanie 5.58
87Zadanie 5.60
87Zadanie 5.62
87Zadanie 5.63
88Zadanie 5.64
88Zadanie 5.65
88Zadanie 5.66
88Zadanie 5.67
88Zadanie 5.68
88Zadanie 5.69
88Zadanie 5.70
88Zadanie 5.71
89Zadanie 5.72
89Zadanie 5.73
89Zadanie 5.74
89Zadanie 5.75
89Zadanie 5.76
89Zadanie 5.77
90Zadanie 5.78
90Zadanie 5.79
90Zadanie 5.80
90Zadanie 5.81
91Zadanie 5.82
91Zadanie 5.83
91Zadanie 5.85
91Zadanie 5.86
92Zadanie 5.87
92Zadanie 5.88
92Zadanie 5.100
93Zadanie 5.102
94Zadanie 5.107
94Zadanie 5.112
95Zadanie 5.119
96Zadanie 5.120
96Zadanie 5.122
96Zadanie 5.127
97Zadanie 5.130
97Zadanie 5.140
99Zadanie 5.142
99Zadanie 18
102Zadanie 19
102Zadanie 20
102Zadanie 21
102Zadanie 24
103Zadanie 25
103
