Udowodnij, że odcinek SO jest prostopadły do płaszczyzny (ABC), jeśli w trójkącie prostokątnym ABC punkt O jest środkiem przeciwprostokątnej AB. Punkt S nie należy do płaszczyzny (ABC). Wiadomo, że
![]() .
.
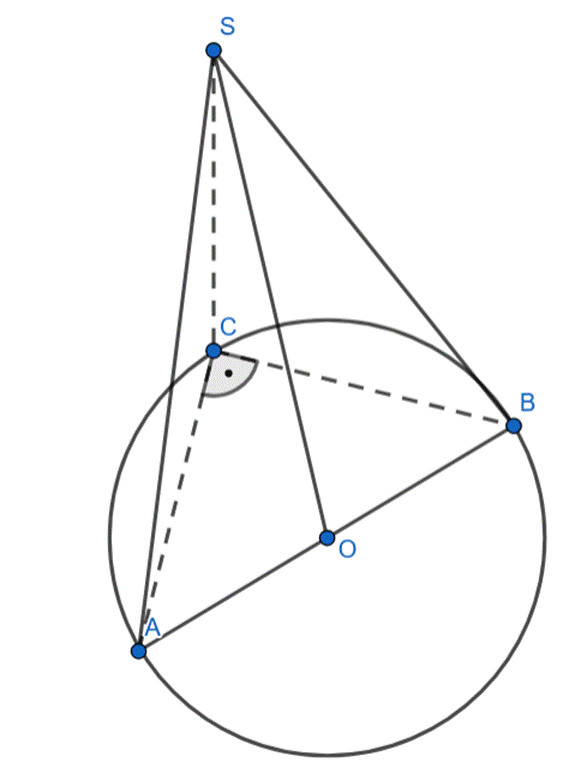
Wszystkie krawędzie boczne ostrosłupa są równe, więc jest to ostrosłup prosty. Spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie ostrosłupa, więc odcinki AO, BO i CO są równej długości, ponieważ są promieniami okręgu o środku O.
Dodatkowo trójkąt ABS jest równoramienny, ponieważ wysokość SO dzieli jego podstawę na pół i ma równe ramiona. Oznacza to, że odcinek SO jest prostopadły do odcinka AB oraz odcinka OC, więc jest prostopadły do całej płaszczyzny ABC.
To kończy dowód.


Zadanie 5.1
78Zadanie 5.2
78Zadanie 5.4
78Zadanie 5.5
78Zadanie 5.6
79Zadanie 5.7
79Zadanie 5.8
79Zadanie 5.35
84Zadanie 5.37
84Zadanie 5.39
84Zadanie 5.40
84Zadanie 5.41
85Zadanie 5.42
85Zadanie 5.45
85Zadanie 5.46
85Zadanie 5.47
86Zadanie 5.50
86Zadanie 5.53
86Zadanie 5.55
87Zadanie 5.56
87Zadanie 5.57
87Zadanie 5.58
87Zadanie 5.60
87Zadanie 5.62
87Zadanie 5.63
88Zadanie 5.64
88Zadanie 5.65
88Zadanie 5.66
88Zadanie 5.67
88Zadanie 5.68
88Zadanie 5.69
88Zadanie 5.70
88Zadanie 5.71
89Zadanie 5.72
89Zadanie 5.73
89Zadanie 5.74
89Zadanie 5.75
89Zadanie 5.76
89Zadanie 5.77
90Zadanie 5.78
90Zadanie 5.79
90Zadanie 5.80
90Zadanie 5.81
91Zadanie 5.82
91Zadanie 5.83
91Zadanie 5.85
91Zadanie 5.86
92Zadanie 5.87
92Zadanie 5.88
92Zadanie 5.100
93Zadanie 5.102
94Zadanie 5.107
94Zadanie 5.112
95Zadanie 5.119
96Zadanie 5.120
96Zadanie 5.122
96Zadanie 5.127
97Zadanie 5.130
97Zadanie 5.140
99Zadanie 5.142
99Zadanie 18
102Zadanie 19
102Zadanie 20
102Zadanie 21
102Zadanie 24
103Zadanie 25
103
