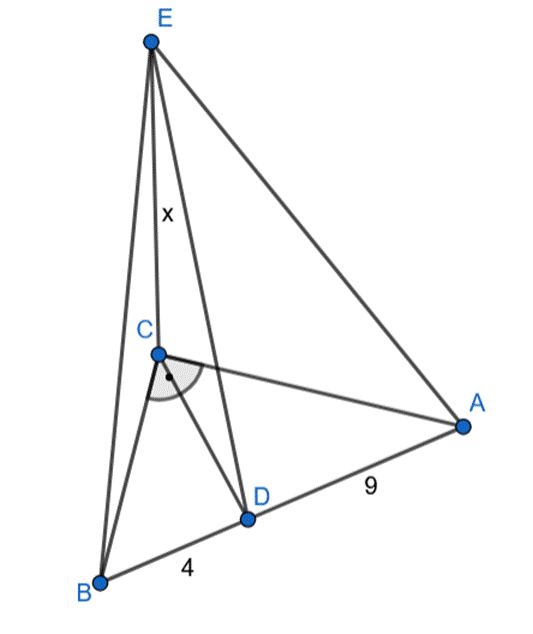
Wyznacz odległość punktu E od płaszczyzny (ABC), jeśli w trójkącie prostokątnym ABC wysokość CD poprowadzona na przeciwprostokątną AB dzieli ją na odcinki długości:
![]() i
i
![]() , odcinek EC jest prostopadły do płaszczyzny (ABC), a pole trójkąta ABC jest o
, odcinek EC jest prostopadły do płaszczyzny (ABC), a pole trójkąta ABC jest o
![]() mniejsze od pola trójkąta ABE,
mniejsze od pola trójkąta ABE,
![]()
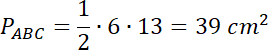
![]()
Rzutem prostopadłym odcinka DE jest odcinek DC, odcinki AB oraz CD są prostopadłe, więc korzystając z twierdzenia o trzech prostych prostopadłych: rzut odcinka DE jest prostopadły do odcinka AB, więc odcinek DE jest wysokością trójkąta ABE.
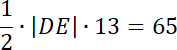
![]()
![]()
![]()
![]()
![]()

Wykonaj rysunek pomocniczy i skorzystaj ze wzoru na wysokość w trójkącie prostokątnym:
![]() , gdzie
, gdzie
![]() i
i
![]() , to odcinki na jakie wysokość podzieliła przeciwprostokątną trójkąta prostokątnego. Następnie skorzystaj z twierdzenia o trzech prostych prostopadłych: jeśli rzut prostopadły danej prostej
, to odcinki na jakie wysokość podzieliła przeciwprostokątną trójkąta prostokątnego. Następnie skorzystaj z twierdzenia o trzech prostych prostopadłych: jeśli rzut prostopadły danej prostej
![]() jest prostopadły do pewnej prostej
jest prostopadły do pewnej prostej
![]() , to prosta
, to prosta
![]() jest również prostopadła do prostej
jest również prostopadła do prostej
![]() .
.
Następnie zauważ, że trójkąt CDE jest prostokątny. Skorzystaj z twierdzenia Pitagorasa, aby obliczyć długość odcinka
![]() .
.

Zadanie 5.1
78Zadanie 5.2
78Zadanie 5.4
78Zadanie 5.5
78Zadanie 5.6
79Zadanie 5.7
79Zadanie 5.8
79Zadanie 5.35
84Zadanie 5.37
84Zadanie 5.39
84Zadanie 5.40
84Zadanie 5.41
85Zadanie 5.42
85Zadanie 5.45
85Zadanie 5.46
85Zadanie 5.47
86Zadanie 5.50
86Zadanie 5.53
86Zadanie 5.55
87Zadanie 5.56
87Zadanie 5.57
87Zadanie 5.58
87Zadanie 5.60
87Zadanie 5.62
87Zadanie 5.63
88Zadanie 5.64
88Zadanie 5.65
88Zadanie 5.66
88Zadanie 5.67
88Zadanie 5.68
88Zadanie 5.69
88Zadanie 5.70
88Zadanie 5.71
89Zadanie 5.72
89Zadanie 5.73
89Zadanie 5.74
89Zadanie 5.75
89Zadanie 5.76
89Zadanie 5.77
90Zadanie 5.78
90Zadanie 5.79
90Zadanie 5.80
90Zadanie 5.81
91Zadanie 5.82
91Zadanie 5.83
91Zadanie 5.85
91Zadanie 5.86
92Zadanie 5.87
92Zadanie 5.88
92Zadanie 5.100
93Zadanie 5.102
94Zadanie 5.107
94Zadanie 5.112
95Zadanie 5.119
96Zadanie 5.120
96Zadanie 5.122
96Zadanie 5.127
97Zadanie 5.130
97Zadanie 5.140
99Zadanie 5.142
99Zadanie 18
102Zadanie 19
102Zadanie 20
102Zadanie 21
102Zadanie 24
103Zadanie 25
103
