Udowodnij, że trójkąty ABE oraz BCE są prostokątne, jeśli dany jest kwadrat ABCD, a odcinek DE jest prostopadły do płaszczyzny (ABCD).
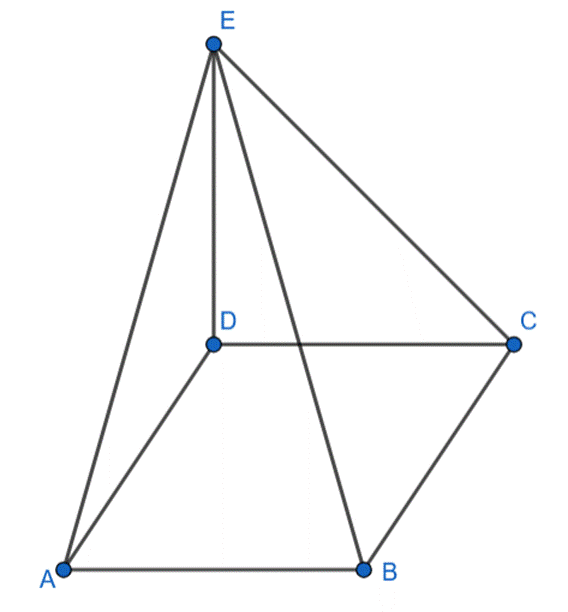
Rzutem odcinka EC jest odcinek CD, a rzutem odcinek AE jest odcinek AD. Ponieważ figura ABCD jest kwadratem, to odcinki BC i CD oraz AB i AD są do siebie prostopadłe. Korzystając z twierdzenia o trzech prostych prostopadłych: aby odcinek CB był prostopadły do odcinka CE, to musi być prostopadły do odcinka CD – jest tak, analogicznie: aby odcinek AB był prostopadły do odcinka AE, to musi być prostopadły do odcinka AD. Więc trójkąty BCE i ABE są prostokątne.
To kończy dowód.

Skorzystaj z twierdzenia o trzech prostych prostopadłych: jeśli rzut prostopadły danej prostej
![]() jest prostopadły do pewnej prostej
jest prostopadły do pewnej prostej
![]() , to prosta
, to prosta
![]() jest również prostopadła do prostej
jest również prostopadła do prostej
![]() .
.

Zadanie 5.1
78Zadanie 5.2
78Zadanie 5.4
78Zadanie 5.5
78Zadanie 5.6
79Zadanie 5.7
79Zadanie 5.8
79Zadanie 5.35
84Zadanie 5.37
84Zadanie 5.39
84Zadanie 5.40
84Zadanie 5.41
85Zadanie 5.42
85Zadanie 5.45
85Zadanie 5.46
85Zadanie 5.47
86Zadanie 5.50
86Zadanie 5.53
86Zadanie 5.55
87Zadanie 5.56
87Zadanie 5.57
87Zadanie 5.58
87Zadanie 5.60
87Zadanie 5.62
87Zadanie 5.63
88Zadanie 5.64
88Zadanie 5.65
88Zadanie 5.66
88Zadanie 5.67
88Zadanie 5.68
88Zadanie 5.69
88Zadanie 5.70
88Zadanie 5.71
89Zadanie 5.72
89Zadanie 5.73
89Zadanie 5.74
89Zadanie 5.75
89Zadanie 5.76
89Zadanie 5.77
90Zadanie 5.78
90Zadanie 5.79
90Zadanie 5.80
90Zadanie 5.81
91Zadanie 5.82
91Zadanie 5.83
91Zadanie 5.85
91Zadanie 5.86
92Zadanie 5.87
92Zadanie 5.88
92Zadanie 5.100
93Zadanie 5.102
94Zadanie 5.107
94Zadanie 5.112
95Zadanie 5.119
96Zadanie 5.120
96Zadanie 5.122
96Zadanie 5.127
97Zadanie 5.130
97Zadanie 5.140
99Zadanie 5.142
99Zadanie 18
102Zadanie 19
102Zadanie 20
102Zadanie 21
102Zadanie 24
103Zadanie 25
103
