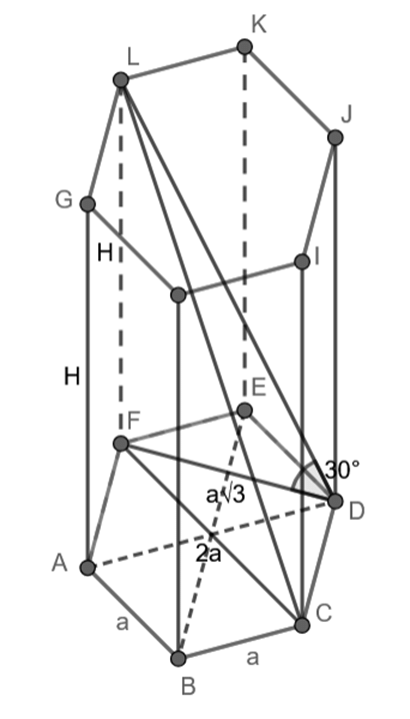
Wyznacz pole powierzchni bocznej i objętość graniastosłupa, jeśli w graniastosłupie prawidłowym sześciokątnym dłuższa przekątna ma długość
![]() dm, a krótsza przekątna jest nachylona do płaszczyzny podstawy pod kątem 30°
dm, a krótsza przekątna jest nachylona do płaszczyzny podstawy pod kątem 30°
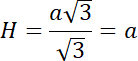
![]()
![]()
![]()
![]()
![]()
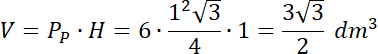

Skorzystaj z tego, że wysokość trójkąta równobocznego o boku
![]() ma długość
ma długość
![]() i zauważ, że trójkąt prostokątny o kątach
i zauważ, że trójkąt prostokątny o kątach
![]() jest szczególny - długość boku naprzeciwko największego kąta jest dwa razy większa od długości boku naprzeciwko najkrótszego kąta, a długość boku naprzeciwko średniego kąta jest
jest szczególny - długość boku naprzeciwko największego kąta jest dwa razy większa od długości boku naprzeciwko najkrótszego kąta, a długość boku naprzeciwko średniego kąta jest
![]() razy dłuższa od długości boku naprzeciwko najmniejszego kąta. Na tej podstawie oblicz długość wysokości graniastosłupa. Następnie skorzystaj z twierdzenia Pitagorasa, aby obliczyć wartość
razy dłuższa od długości boku naprzeciwko najmniejszego kąta. Na tej podstawie oblicz długość wysokości graniastosłupa. Następnie skorzystaj z twierdzenia Pitagorasa, aby obliczyć wartość
![]() . Na koniec obliczy objętość tej bryły.
. Na koniec obliczy objętość tej bryły.

Zadanie 5.1
78Zadanie 5.2
78Zadanie 5.4
78Zadanie 5.5
78Zadanie 5.6
79Zadanie 5.7
79Zadanie 5.8
79Zadanie 5.35
84Zadanie 5.37
84Zadanie 5.39
84Zadanie 5.40
84Zadanie 5.41
85Zadanie 5.42
85Zadanie 5.45
85Zadanie 5.46
85Zadanie 5.47
86Zadanie 5.50
86Zadanie 5.53
86Zadanie 5.55
87Zadanie 5.56
87Zadanie 5.57
87Zadanie 5.58
87Zadanie 5.60
87Zadanie 5.62
87Zadanie 5.63
88Zadanie 5.64
88Zadanie 5.65
88Zadanie 5.66
88Zadanie 5.67
88Zadanie 5.68
88Zadanie 5.69
88Zadanie 5.70
88Zadanie 5.71
89Zadanie 5.72
89Zadanie 5.73
89Zadanie 5.74
89Zadanie 5.75
89Zadanie 5.76
89Zadanie 5.77
90Zadanie 5.78
90Zadanie 5.79
90Zadanie 5.80
90Zadanie 5.81
91Zadanie 5.82
91Zadanie 5.83
91Zadanie 5.85
91Zadanie 5.86
92Zadanie 5.87
92Zadanie 5.88
92Zadanie 5.100
93Zadanie 5.102
94Zadanie 5.107
94Zadanie 5.112
95Zadanie 5.119
96Zadanie 5.120
96Zadanie 5.122
96Zadanie 5.127
97Zadanie 5.130
97Zadanie 5.140
99Zadanie 5.142
99Zadanie 18
102Zadanie 19
102Zadanie 20
102Zadanie 21
102Zadanie 24
103Zadanie 25
103
