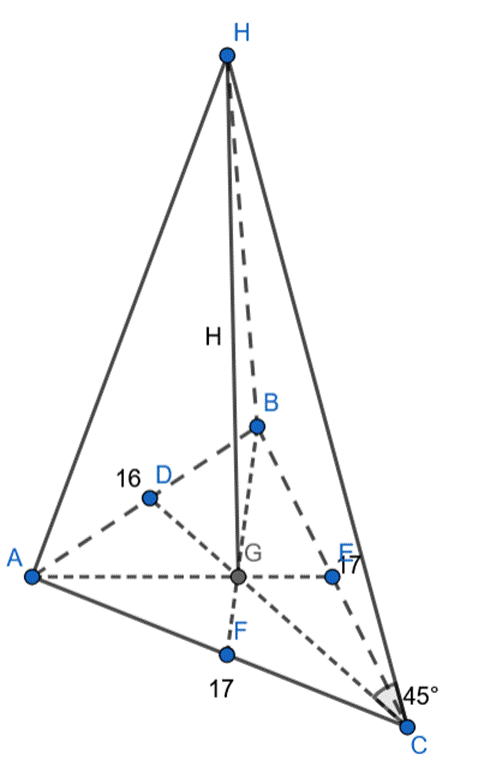
Wyznacz wysokość ostrosłupa, jeśli podstawą ostrosłupa jest trójkąt równoramienny, którego dwa boki mają długość 17 cm, a długość trzeciego boku jest równa 16 cm. Wszystkie krawędzie boczne tego ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 45°.
![]()
![]()
![]()
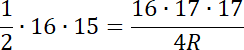
![]()
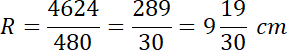
![]()
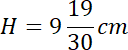

Skorzystaj z twierdzenia Pitagorasa i oblicz długość wysokości podstawy.
Zauważ, że skoro wszystkie krawędzie boczne tworzą taki sam kąt z podstawą, to znaczy, że wszystkie mają jednakową długość i że spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie. Skorzystaj ze wzoru na pole trójkąta z promieniem okręgu opisanego i wyznacz jego długość. Zauważ, że trójkąt prostokątny o kątach
![]() jest szczególny – jest połową kwadratu.
jest szczególny – jest połową kwadratu.

Zadanie 5.1
78Zadanie 5.2
78Zadanie 5.4
78Zadanie 5.5
78Zadanie 5.6
79Zadanie 5.7
79Zadanie 5.8
79Zadanie 5.35
84Zadanie 5.37
84Zadanie 5.39
84Zadanie 5.40
84Zadanie 5.41
85Zadanie 5.42
85Zadanie 5.45
85Zadanie 5.46
85Zadanie 5.47
86Zadanie 5.50
86Zadanie 5.53
86Zadanie 5.55
87Zadanie 5.56
87Zadanie 5.57
87Zadanie 5.58
87Zadanie 5.60
87Zadanie 5.62
87Zadanie 5.63
88Zadanie 5.64
88Zadanie 5.65
88Zadanie 5.66
88Zadanie 5.67
88Zadanie 5.68
88Zadanie 5.69
88Zadanie 5.70
88Zadanie 5.71
89Zadanie 5.72
89Zadanie 5.73
89Zadanie 5.74
89Zadanie 5.75
89Zadanie 5.76
89Zadanie 5.77
90Zadanie 5.78
90Zadanie 5.79
90Zadanie 5.80
90Zadanie 5.81
91Zadanie 5.82
91Zadanie 5.83
91Zadanie 5.85
91Zadanie 5.86
92Zadanie 5.87
92Zadanie 5.88
92Zadanie 5.100
93Zadanie 5.102
94Zadanie 5.107
94Zadanie 5.112
95Zadanie 5.119
96Zadanie 5.120
96Zadanie 5.122
96Zadanie 5.127
97Zadanie 5.130
97Zadanie 5.140
99Zadanie 5.142
99Zadanie 18
102Zadanie 19
102Zadanie 20
102Zadanie 21
102Zadanie 24
103Zadanie 25
103
