![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ODP: Wartości
![]() spełniające warunki zadania należą do zbioru
spełniające warunki zadania należą do zbioru
![]()

Zauważ, że aby równanie miało dwa rozwiązania, to
![]() . Oblicz ją.
. Oblicz ją.
![]()
Zauważ wzór skróconego mnożenia na różnicę kwadratów.
![]()
Oblicz wartości
![]() , dla których każdy z nawiasów się zeruję.
, dla których każdy z nawiasów się zeruję.
![]()
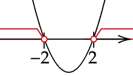
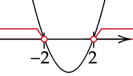
Zaznacz uzyskane rozwiązania na osi. Ramiona paraboli skieruj do góry, ponieważ współczynnik przy najwyższej potędze jest dodatni. Zaznacz przedziały w których wykres jest nad osią.
![]()
Pozostało rozwiązać przypadek, gdy każde z rozwiązań należy do przedziału
![]() , czyli jest mniejsze od 3.
, czyli jest mniejsze od 3.
![]()
Zapisz wzór na większe miejsce zerowe funkcji (skoro większe z rozwiązań jest mniejsze od 3, to drugie tym bardziej) i podstaw znane wartości.
![]()
![]()
![]()
![]()
Zauważ, że aby móc podnieść całą nierówność do kwadratu i pozbyć się pierwiastka, to wartość znajdująca się z prawej strony nierówności musi być nieujemna.
Oblicz dla jakich
![]() wartość z prawej strony nierówności jest większa lub równa zero.
wartość z prawej strony nierówności jest większa lub równa zero.
![]()
![]()
![]()
Podnieś całą nierówność do kwadratu i przenieś wszystkie wartości na lewą stronę.
![]()
![]()
![]()
![]()
Oblicz rozwiązania powstałej nierówności, czyli deltę i miejsca zerowe.
![]()
![]()
![]()
![]()
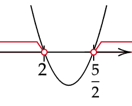
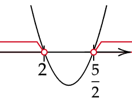
Zaznacz uzyskane rozwiązania na osi. Ramiona paraboli skieruj do góry, ponieważ współczynnik przy najwyższej potędze jest dodatni. Zaznacz przedziały w których wykres jest nad osią.
![]()
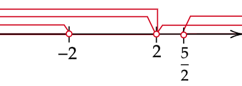
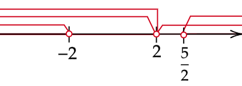
Zaznacz na osi wszystkie
![]() spełniające warunki zadania.
spełniające warunki zadania.
![]()
Oznacza to, że nierówność jest spełniona dla
![]() .
.