Arkusz egzaminacyjny, Wydawnictwo: CKE

Zadanie 14 - strona 14

Oblicz pole koła wpisanego w trójkąt ABP powstałego przez przecięcie przekątnych AC i BD trapezu równoramiennego ABCD w punkcie P, jeśli jego ramię na długość 6, a dłuższa podstawa AB – 12 i jest średnicą okręgu opisanego na trapezie.

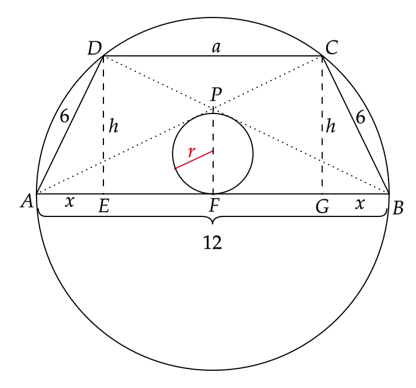
Trójkąty ADB i ACB są przystające i prostokątne.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Trójkąty DEB i PFB są podobne z cechy kąt, kąt, kąt.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

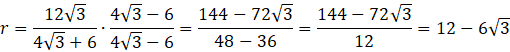
ODP: Pole koła wpisanego w trójkąt ABP wynosi $\text{[math]}$

Wykonaj rysunek pomocniczy.

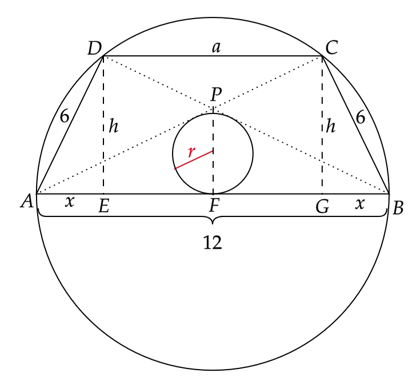
Zauważ, że skoro odcinek AB jest średnicą okręgu, to trójkąty ADB i ACB są przystające i prostokątne.

Skorzystaj z twierdzenia Pitagorasa w trójkącie ABD i oblicz długość przekątnej trapezu BD.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Skorzystaj z dwóch wzorów na pole trójkąta ABD. Podstaw znane wartości i oblicz wysokość trapezu.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Skorzystaj z twierdzenia Pitagorasa w trójkącie ADE i oblicz długość odcinka $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Oblicz długość krótszej podstawy trapezu.

$\text{[math]}$

Zauważ, że trójkąty DEB i PFB są podobne z cechy kąt, kąt, kąt $\text{[math]}$ , więc $\text{[math]}$

Skorzystaj z tego podobieństwa oblicz długość boku FB, czyli wysokości trójkąta ABP.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Ponownie skorzystaj z twierdzenia Pitagorasa w trójkącie BPF i oblicz długość odcinka BP.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Oblicz obwód trójkąta ABP i połowę jego wartości.

$\text{[math]}$

$\text{[math]}$

Skorzystaj z dwóch wzorów na pole trójkąta ABP. Podstaw znane wartości i oblicz promień kola wpisanego w trójkąt ABP.

$\text{[math]}$

$\text{[math]}$

Pamiętaj o usunięciu niewymierności z mianownika.

$\text{[math]}$

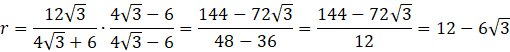
Znasz już promień koła wpisanego w trójkąt ABP. Oblicz jego pole.

$\text{[math]}$

Ćwiczenie 2, strona 240, Matematyka. Klasa 2. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Ćwiczenie 6., strona 88, Matematyka. Klasa 5. Podręcznik. Część 2 – rozwiązania i odpowiedzi

Zadanie 2.110., strona 40, Matematyka. Klasa 3. Zbiór zadań. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 3, strona 107, NOWA MATeMAtyka 1. Podręcznik. Zakres podstawowy

Zadanie 6, strona 374, Matematyka. Klasa 2. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 10., strona 52, Matematyka z kluczem. Klasa 6. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie 4., strona 85, Matematyka z plusem. Klasa 8. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 5, strona 124, MATeMAtyka. Klasa 3. Zbiór zadań. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Ćwiczenie 11., strona 85, Matematyka. Klasa 4. Podręcznik – rozwiązania i odpowiedzi

Zadanie 10, strona 263, MATeMAtyka. Klasa 3. Zbiór zadań. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

2

2

2

2

2

4

5

6

7

8

9

10

12

14

16

Pełny spis treści